Cho tứ giác ABCD có E,F,G,H lần lượt là trung điểm của AB,BC,CD,DA

Bài 39 trang 103 SBT Toán 8 Tập 1: Cho tứ giác $ABCD$ có $E,F,G,H$ lần lượt là trung điểm của $AB,BC,CD,DA$. Điều kiện của tứ giác $ABCD$ để tứ giác $EFGH$ là hình chữ nhật là:

A.  $BD=AC$

B.  $AB\mathrm{\perp }BC$

C.  $BD\mathrm{\perp }AC$

D.  $AB=CD$

Trả lời

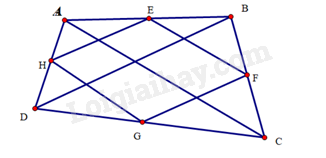
Nối $AC,BD$

Xét tam giác $ABCD$ có $E,H$ lần lượt là trung điểm của $AB,AD$ nên $EH$ là đường trung bình của tam giác $ABD$.

Suy ra $EH//BD,EH=\frac{1}{2}BD$ (1)

Tương tự xét tam giác $CBD$ có $F,G$ lần lượt là trung điểm của $BC,CD$ nên $Fg$ là đường trung bình của tam giác $CBD$ suy ra $FG//BD,FG=\frac{1}{2}BD$ (2)

Từ (1), (2) suy ra $EH//FG;EH=FG$ nên $EFGH$ là hình bình hành (dấu hiệu nhận biết).

Để hình bình hành $EFGH$ là hình chữ nhật thì $\widehat{EHG}={90}^{\circ }$ hay $EH\mathrm{\perp }HG$

Lại có $HG//AC$ (do $HG$ là đường trung bình của tam giác $DAC$) nên $EH\mathrm{\perp }AC$ mà $EH\mathrm{\perp }BD$ (cmt) nên $AC\mathrm{\perp }BD$.

Vậy tứ giác $ABCD$ cần có $AC\mathrm{\perp }BD$ thì $EFGH$ là hình chữ nhật.

→   Đáp án đúng là đáp án C.

Xem thêm các bài giải SBT Toán 8 Cánh diều hay, chi tiết khác:

Bài 3: Hình thang cân

Bài 4: Hình bình hành

Bài 5: Hình chữ nhật

Bài 6: Hình thoi

Bài 7: Hình vuông

Bài tập cuối chương 5 trang 103