Giải SBT Toán 8 Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến
Giải SBT Toán 8 trang 7
Bài 1 trang 7 SBT Toán 8 Tập 1: a) Trong các biểu thức sau, biểu thức nào là đơn thức?
√211x;-3x+y4;-3xy4z;-1321x3y5+7.
b) Trong các biểu thức sau, biểu thức nào là đa thức?
-1321x3y2+9xy6-8;x+y;xyz+√2;x-5zx2+z2+1.
Lời giải:
a) Các biểu thức là đơn thức là: √211x;-3xy4z.
b) Các biểu thức là đa thức là: -1321x3y2+9xy6-8;x+y;xyz+√2.
Bài 2 trang 7 SBT Toán 8 Tập 1: Thu gọn mỗi đơn thức sau:
a) -917x23y22y14.
b) 2√121xy3zy2z3.
c) -187124x4y6z8x5y2z10.
Lời giải:
a) -917x23y22y14=-917x23(y22.y14)=-917x23y36.
b) 2√121xy3zy2z3=2√112x(y3.y2)(z.z3)=211xy5z4.
c) -187124x4y6z8x5y2z10=-187124(x4.x5)(y6.y2)(z8.z10)=-187124x9y8z18.
Giải SBT Toán 8 trang 8
Bài 3 trang 8 SBT Toán 8 Tập 1: Thực hiện phép tính:
a) xy3 ‒ 2xy3 ‒ 12xy3;
b) -1243x2y+2x2y+-3143x2y;
c) -√1675x6y9z+-√4915x6y9z-15x6y9z.
Lời giải:
a) xy3 ‒ 2xy3 ‒ 12xy3 = (1 ‒ 2 ‒ 12)xy3 = ‒13xy3.
b) -1243x2y+2x2y+-3143x2y
=(-1243+-3143+2)x2y
= (‒1 + 2)x2y
= x2y.
c) -√1675x6y9z+-√4915x6y9z-15x6y9z
=-475x6y9z-715x6y9z-15x6y9z
=(-475-715-15)x6y9z
=(-475-3575-1575)x6y9z=-5475x6y9z=-1825x6y9z.
Bài 4 trang 8 SBT Toán 8 Tập 1: Thu gọn mỗi đa thức sau:
a) x2y5+2xy2-x2y5+2435xy2;
b) ‒11y2z3 ‒ 22xy3z3 + 2y2z3 ‒ 33xy3z3 ‒ 72;
c) √441x2y4z3+x2y4z+3941x2y4z3-x2y4z+z18.
Lời giải:
a) x2y5+2xy2-x2y5+2435xy2
=(x2y5-x2y5)+(2xy2+2435xy2)
=0+(2+2435)xy2
=9435xy2.
b) ‒11y2z3 ‒ 22xy3z3 + 2y2z3 ‒ 33xy3z3 ‒ 72
= (‒11y2z3 + 2y2z3) + (‒22xy3z3 ‒ 33xy3z3) ‒ 72
= ‒9y2z3 ‒ 55xy3z3 ‒ 72.
c) √441x2y4z3+x2y4z+3941x2y4z3-x2y4z+z18
=241x2y4z3+x2y4z+3941x2y4z3-x2y4z+z18
=(241x2y4z3+3941x2y4z3)+(x2y4z-x2y4z)+z18
=x2y4z3+z18.
Bài 5 trang 8 SBT Toán 8 Tập 1: Tính giá trị của mỗi biểu thức sau:
a) A=-x3y2+2x2y5-12xy tại x=2;y=12;
b) B=y12+x5y5-100x4y4+100x3y3-100x2y2+100xy-√36 tại x = 99, y = 0;
c) C=xy2+52xz-√3xyz3+25 tại x=-12;y=-√3;z=2.
Lời giải:
a) Thay x=2;y=12 vào A, ta có:
A=-23.(12)2+2.22.(12)5-12.2.12
=-23.122+23.125-12=-2+14-12=-94.
b) Thay x = 99 và y = 0 vào B, ta có:
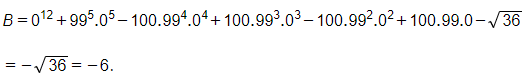
c) Thay x=-12;y=-√3;z=2 vào C ta có:
C=-12.(-√3)2+52.-12.2-√3.-12.(-√3).23+25
=-12.3+25.(-1)+3.(-1).22+25=-32-25-12+25=-272.
Lời giải:
Do 54 ⋮ 2; 36 ⋮ 2; 12 ⋮ 2; 6 ⋮ 2nên (‒54y6 + 36y4 +12y2 ‒ 6y)⋮ 2.
Suy ra giá trị của đa thức K = ‒54y6 + 36y4 +12y2 ‒ 6ylà số chẵn tại mọi số nguyên y. Mà 23 là số lẻ, suy ra giá trị của đa thức H = ‒54y6 + 36y4 +12y2 6y + 23là số lẻ tại mọi số nguyên y.
Lời giải:
Ta có: G=12x2+bx+23=12x2-12x+12x+bx+23
=(12x2-12x)+(12x+bx)+23
=x2-x2+(12+b)x+23
=(x-1)x2+(12+b)x+23.
Do trong hai số nguyên liên tiếp luôn có một số chia hết cho 2 nên (x-1)x2 luôn nhận giá trị nguyên tại mọi số nguyên x.
Mà 12+b là số nguyên, suy ra (x-1)x2+(12+b)x+23 luôn nhận giá trị nguyên tại mọi số nguyên x.
Vậy G luôn nhận giá trị nguyên tại mọi số nguyên x.
Xem thêm lời giải SBT Toán 8 sách Cánh diều hay, chi tiết khác:
Bài 2: Các phép tính với đa thức nhiều biến
Bài 3: Hằng đẳng thức đáng nhớ
Bài 4: Vận dụng hằng đẳng thức vào phân tích đa thức thành nhân tử




