Cho tam giác ABC vuông tại A có đường cao AH. Kẻ HJ vuông góc với AB tại J và K vuông góc với AC tại K

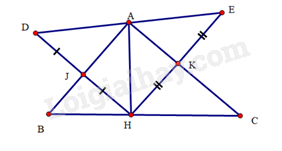
Bài 41 trang 104 SBT Toán 8 Tập 1: Cho tam giác $ABC$ vuông tại $A$ có đường cao $AH$. Kẻ $HJ$ vuông góc với $AB$ tại $J$ và $HK$ vuông góc với $AC$ tại $K$. Trên tia $HJ$ lấy điểm $D$ sao cho $DJ=JH$. Trên tia $HK$ lấy điểm $E$ sao cho $EK=KH$.

a) Chứng minh $A$ là trung điểm của $DE$.

b) Tứ giác $AJHK$ là hình gì? Vì sao?

c) Chứng minh $BC=BD+CE$.

Trả lời

a)  Xét $\mathrm{\Delta }ADJ$ vuông tại $J$ và $\mathrm{\Delta }AHJ$ vuông tại $J$ có:

$DJ=HJ$ (gt), $AJ$ là cạnh chung

Do đó $\mathrm{\Delta }ADJ=\mathrm{\Delta }AHJ$ (hai cạnh góc vuông)

Suy ra $AD=AH$ (hai cạnh tương ứng) và $\widehat{JAD}=\widehat{JAH}$ (hai góc tương ứng)

Tương tự ta cũng chứng minh được $\mathrm{\Delta }AHK=\mathrm{\Delta }AEk$ (hai cạnh góc vuông)

Suy ra $AH=AE$ (hai cạnh tương ứng) và $\widehat{KAH}=\widehat{KAE}$ (hai góc tương ứng)

Ta có:

$\widehat{JAD}+\widehat{JAH}+\widehat{KAH}+\widehat{KAE}=2\left(\widehat{JAH}+\widehat{KAH}\right)=2.\widehat{JAK}={2.90}^{\circ }={180}^{\circ }$

Hay $\widehat{DAE}={180}^{\circ }$ nên ba điểm $D,A,E$ thẳng hàng

Lại có $AD=AH$ và $AH=AE$ nên $AD=AE$

Do đó $A$ là trung điểm của $DE$.

b) Ta có $AB\mathrm{\perp }HE$ tại $K$ nên $\widehat{AJH}={90}^{\circ }$

$AC\mathrm{\perp }HE$ tại $K$ nên $\widehat{AKH}={90}^{\circ }$

Xét tứ giác $AJKH$ có:

$\widehat{AJH}=\widehat{JAK}=\widehat{AKH}={90}^{\circ }$ nên là hình chữ nhật.

c) Xét tam giác $BDJ$ vuông tại $J$ và tam giác $BHJ$ vuông tại $J$ có:

$DJ=HJ$ (gt), $BJ$ là cạnh chung

Do đó $\mathrm{\Delta }BDJ=\mathrm{\Delta }BHJ$ (hai cạnh góc vuông)

Suy ra $BD=BH$ (hai cạnh tương ứng)

Tương tự, ta cũng có $\mathrm{\Delta }CHK=\mathrm{\Delta }CEK$ (hai cạnh góc vuông)

Suy ra $CH=CE$ (hai cạnh tương iwnsg)

Khi đó $BC=BH+CH=BD+CE$

Vậy $BC=BD+CE$.

Xem thêm các bài giải SBT Toán 8 Cánh diều hay, chi tiết khác:

Bài 3: Hình thang cân

Bài 4: Hình bình hành

Bài 5: Hình chữ nhật

Bài 6: Hình thoi

Bài 7: Hình vuông

Bài tập cuối chương 5 trang 103