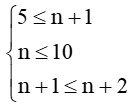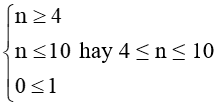Giải SBT Toán 8 (Cánh diều) Bài 2: Các phép tính với đa thức nhiều biến

Giải SBT Toán 8 Bài 2: Các phép tính với đa thức nhiều biến

Giải SBT Toán 8 trang 11

Bài 8 trang 11 SBT Toán 8 Tập 1: Cho hai đa thức: A = x⁷ ‒ 4x³y² ‒ 5xy + 7; B = x⁷ + 5x³y² ‒ 3xy ‒ 3.

a) Tìm đa thức C sao cho C = A + B.

b) Tìm đa thức D sao cho A + D = B.

Lời giải:

a) C = A + B = x⁷ ‒ 4x³y² ‒ 5xy + 7 + x⁷ + 5x³y² ‒ 3xy ‒ 3

= (x⁷ + x⁷) + (‒ 4x³y² + 5x³y²) + (‒ 5xy ‒ 3xy) + 4

= 2x⁷ + x³y² ‒ 8xy + 4.

Vậy C = 2x⁷ + x³y² ‒ 8xy + 4.

b) Ta có A + D = B

Suy ra D = B ‒ A

= x⁷ + 5x³y² ‒ 3xy ‒ 3 ‒ (x⁷ ‒ 4x³y² ‒ 5xy + 7)

= x⁷ + 5x³y² ‒ 3xy ‒ 3 ‒ x⁷ + 4x³y² + 5xy ‒ 7

= (x⁷ ‒ x⁷) + (5x³y² + 4x³y²) + (‒ 3xy + 5xy) + (–3 – 7)

= 9x³y² + 2xy ‒ 10.

Vậy D = 9x³y² + 2xy ‒ 10.

Bài 9 trang 11 SBT Toán 8 Tập 1: Rút gọn biểu thức:

a) 2x(x² + y) ‒ x(2y + 1) ‒ x(2x² ‒ 21y);

b) 5x(6y ‒ x²) + 3y(y ‒ 10x) ‒ 3y(y ‒ 1) + 15x³;

c) 18xⁿ⁺¹(yⁿ⁺¹ + xⁿ⁺³) + 9y³(‒2xⁿ⁺¹y^n‒2 + 1)với n là số tự nhiên lớn hơn 2.

Lời giải:

a) 2x(x² + y) ‒ x(2y + 1) ‒ x(2x² ‒ 21y)

= 2x³ + 2xy ‒ 2xy ‒ x ‒ 2x³ + 21xy

= (2x³– 2x³) + (2xy ‒ 2xy + 21xy) ‒ x

= 21xy ‒ x.

b) 5x(6y ‒ x²) + 3y(y ‒ 10x) ‒ 3y(y ‒ 1) + 15x³

= 30xy ‒ 5x³ + 3y² ‒ 30xy ‒ 3y² + 3y + 15x³

= (30xy – 30xy) + (‒ 5x³ + 15x³) + (3y² ‒ 3y²) + 3y

= 10x³ + 3y.

c) 18xⁿ⁺¹(yⁿ⁺¹ + xⁿ⁺³) + 9y³(‒2xⁿ⁺¹y^n‒2 + 1)

= 18xⁿ⁺¹yⁿ⁺¹+ 18x^{n+1+ n + 3} – 18xⁿ⁺¹y^{3 + n – 2} + 9y³

= 18xⁿ⁺¹yⁿ⁺¹ + 18x²ⁿ⁺⁴ ‒ 18xⁿ⁺¹yⁿ⁺¹ + 9y³

= 18x²ⁿ⁺⁴ + 9y³.

Giải SBT Toán 8 trang 12

Bài 10 trang 12 SBT Toán 8 Tập 1: Tìm ba số tự nhiên liên tiếp, biết tích của hai số sau lớn hơn tích của hai số trước là 12 đơn vị.

Lời giải:

Gọi ba số tự nhiên liên tiếp cần tìm là a, a + 1, a + 2.

Do tích của hai số sau lớn hơn tích của hai số trước là 12 đơn vị nênta có:

(a + 1)(a + 2) ‒ a(a + 1) = 12.

Do đó a² + 2a + a + 2 ‒ a² ‒ a = 12

Hay 2a = 10

Suy ra a = 5

Vậy 3 số cần tìm là: 5; 6; 7.

Bài 11 trang 12 SBT Toán 8 Tập 1: Chứng minh giá trị của mỗi biểu thức sau không phụ thuộc vào giá trị của biến:

a) M = (x ‒ 1)(x² + x + 1) ‒ x²(x ‒ 1) ‒ x² ‒ 23;

b) $N=\left(x-\frac{1}{2}y\right)\left(x^2+2y\right)-x\left(x^2+2y\right)+y\left(\frac{1}{2}{x}^2+y\right)-\frac{1}{2}$.

Lời giải:

a) Ta có:

M = (x ‒ 1)(x² + x + 1) ‒ x²(x ‒ 1) ‒ x² ‒ 23

= x³ + x² + x ‒ x² ‒ x ‒ 1 ‒ x³ + x² ‒ x² ‒ 23

= (x³ ‒ x³) + (x² ‒ x²) + (x ‒ x) + (‒1 ‒ 23)

= ‒24.

Vậy giá trị của M không phụ thuộc vào giá trị của biến.

b) Ta có:

$N=\left(x-\frac{1}{2}y\right)\left(x^2+2y\right)-x\left(x^2+2y\right)+y\left(\frac{1}{2}{x}^2+y\right)-\frac{1}{2}$

$=x^3+2xy-\frac{1}{2}{x}^{2}y-y^2-x^3-2xy+\frac{1}{2}{x}^{2}y+y^2-\frac{1}{2}=-\frac{1}{2}$

Vậy giá trị của Nkhông phụ thuộc vào giá trị của biến.

Bài 12 trang 12 SBT Toán 8 Tập 1: Chứng minh rằng biểu thức P = (2y ‒ x)(x + y) + x(y ‒ x) ‒ 2y(x + 5y) ‒ 1 luôn nhận giá trị âm với mọi giá trị của biến x và y.

Lời giải:

Ta có:

P = (2y ‒ x)(x + y) + x(y ‒ x) ‒ 2y(x + 5y) ‒ 1

= 2xy + 2y² ‒ x² ‒ xy +xy ‒ x² ‒ 2xy ‒ 10y² ‒ 1

= (2xy – xy + xy – 2xy) + (2y² ‒ 10y²) + (‒ x² ‒ x²) – 1

= ‒8y² ‒ 2x² ‒ 1.

Do với mọi giá trị của x, y ta có: x² ≥ 0, y² ≥ 0 nên ‒ 2x² ≤0, ‒8y² ≤0

Suy ra ‒8y² ‒ 2x² ‒ 1≤ ‒1với mọi giá trị của biến x, y.

Vậy P luôn nhận giá trị âm với mọi giá trị của biến x và y.

Bài 13 trang 12 SBT Toán 8 Tập 1: Cho hai đơn thức: A = ‒132xⁿ⁺¹y¹⁰zⁿ⁺²; B = 1,2x⁵yⁿzⁿ⁺¹với n là số tự nhiên.

a) Tìm các số tự nhiên n để đơn thức A chia hết cho đơn thức B.

b) Tìm đa thức P sao cho P = A : B.

c) Tính giá trị của đa thức P tại n = 9; x = 2; y = –1; z = 5,8.

Lời giải:

a) Đơn thức Achia hết cho đơn thức B khi mỗi biến của B đều là biến của A với số mũ không lớn hơn số mũ của nó trong A.

Suy ra 

Do đó 

Mà n ∈ ℕ nên n ∈ {4; 5; 6; 7; 8; 9; 10}.

Vậy n ∈ {4; 5; 6; 7; 8; 9; 10}thì đơn thức Achia hết cho đơn thức B.

b) Ta có: P = A : B

= (‒132xⁿ⁺¹y¹⁰zⁿ⁺²) : (1,2x⁵yⁿzⁿ⁺¹)

= (‒132 : 1,2)(xⁿ⁺¹: x⁵)(y^10‒yⁿ)(zⁿ⁺²: z^{n + 1})

= ‒110x^n+1‒5y^10‒nz^n+2‒n‒1

= ‒110x^n‒4y^10‒nz.

Vậy P = ‒110x^n‒4y^10‒nz.

c) Thay n = 9; x = 2; y = –1; z = 5,8 vào P ta có:

P = ‒110.2^9‒4.(‒1)^10‒9.5,8

= ‒110.2⁵.(–1).5,8

= 110. 32 . 5,8

= 20 416.

Vậy P = 20 416.

Bài 14 trang 12 SBT Toán 8 Tập 1: Một mảnh đất có dạng hình chữ nhật với chiều dài là x (m), chiều rộng là y (m) với 1 < y < x. Người ta để lối đi có độ rộng 1 (m) (phần không tô màu) như Hình 2.

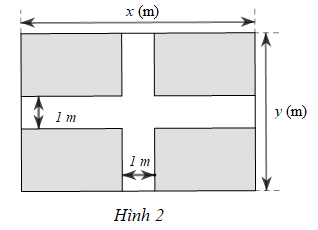
a) Viết đa thức S biểu thị diện tích phần còn lại của mảnh đất đó.

b) Tính giá trị của S tại x = 9; y = 5,4.

Lời giải:

a) Phần còn lại của mảnh đất gồm bốn miếng đất bằng nhau có dạng hình chữ nhật với chiều dài bằng $\frac{x-1}{2}$(m), chiều rộng bằng $\frac{y-1}{2}$(m).

Vậy đa thức biểu thị diện tích phần còn lại của mảnh đất đó là:

$S=4.\frac{x-1}{2}.\frac{y-1}{2}=xy-x-y+1\left(m^2\right)$.

b) Thay x = 9; y = 5,4 vào S ta có:

S = 9.5,4 – 9 – 5,4 +1 = 48,6 – 9 – 5,4 + 1 = 35,2 (m²)

Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác:

Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến

Bài 3: Hằng đẳng thức đáng nhớ

Bài 4: Vận dụng hằng đẳng thức vào phân tích đa thức thành nhân tử

Bài tập cuối chương 1

Bài 1: Phân thức đại số