Cho hình bình hành ABCD có BC = 2AB. Gọi M,N lần lượt là trung điểm của BC,AD

Bài 43 trang 104 SBT Toán 8 Tập 1: Cho hình bình hành $ABCD$ có $BC=2AB$. Gọi $M,N$ lần lượt là trung điểm của $BC,AD$

a) Chứng minh tứ giác $MBND$ là hình bình hành.

b) Gọi $P$ là giao điểm của $AM$ và $BN,Q$ là giao điểm của $CN$ và $DM$. Chứng minh tứ giác $PMQN$ là hình chữ nhật.

c) Tìm điều kiện của hình bình hành $ABCD$ để tứ giác $PMQN$ là hình vuông.

d) Tính diện tích của tứ giác $PMQN$, biết $AB=2cm,\widehat{MAD}={30}^{\circ }$.

Trả lời

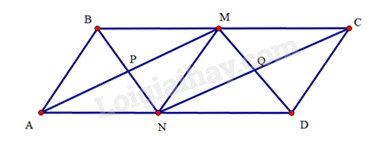
a) Do $ABCD$ là hình bình hành nên $BC//AD$ và $BC=AD$

Mà $M\in BC,N\in AD$ nên $MB//ND$

Lại có $M,N$ lần lượt là trung điểm của $BC,AD$ nên $MB=MC=\frac{1}{2}BC,NA=ND=\frac{1}{2}A$

Do đó $MB=MC=NA=ND$

Tứ goác $MBND$ có $MB//ND$ và $MB=ND$ nên là hình bình hành.

b) Tương tự câu a, ta chứng minh được $MANC$ là hình bình hành.

Do $MBND,MANC$ đều là hình bình hành nên $PN//MQ,PM//NQ$. Suy ra tứ giác $PMQN$ là hình bình hành.

$\mathrm{\Delta }ABN=\mathrm{\Delta }MBN$ (c.g.c). Suy ra $AB=MN$.

Tứ giác $ABMN$ có $AB=BM-MN=AN$ nên $ABMN$ là hình thoi. Suy ra $AM\mathrm{\perp }Bn$

Hình bình hành $PMQN$ có $\widehat{MPN}={90}^{\circ }$ nên $PMQN$ là hình chữ nhật.

c) Để hình chữ nhật $PMQN$ là hình vuông thì $PM=PN$.

Mà $ABMN$ là hình thoi nên $ABMN$ là hình bình hành. Suy ra $AM,BN$ cắt nhau tại trung điểm $P$ của mỗi đường. mà $PM=PN$, suy ra $AM=BN$

Hình bình hành $ABMN$ có $AM=BN$ nên $ABMN$ là hình chữ nhật

Suy ra $\widehat{ABM}={90}^{\circ }$ hay $\widehat{ABC}={90}^{\circ }$

Hình bình hành $ABCD$ có $\widehat{ABC}={90}^{\circ }$ nên $ABCD$ là hình chữ nhật.

Dễ thấy, nếu hình bình hành $ABCD$ là hình chữ nhật và $BC=2AB$ thì $PMQN$ là hình vuông.

Vậy điều kiện của hình bình hành $ABCD$ để $PMQN$ là hình vuông là hình bình hành $ABCD$ là hình chữ nhật có $BC=2AB$.

d) Ta có: $BM=AB$ nên $BM=2cm$

Do $ABMN$ là hình thoi nên $AM$ là tia phân giác của $\widehat{BAN}$

Suy ra $\widehat{BAN}=2\widehat{MAD}={60}^{\circ }$

Tam giác $ABN$ có $AB=AN$ và $\widehat{BAN}={60}^{\circ }$ nên tam giác $ABN$ đều.

Suy ra $BN=AN=AB=2cm$

Do $P$ là trung điểm của $BN$ nên $BP=NP=\frac{BN}{2}=1cm$

Trong tam giác $BMP$ vuông tại $P$, ta có: $B{M}^2=B{P}^2+M{P}^2$

Suy ra $M{P}^2=B{M}^2-B{P}^2=3$. Do đó $MP=\sqrt{3}$ cm

Do $PMQN$ là hình chữ nhật nên diện tích của $PMQN$ là:

$MP.NP=\sqrt{3}.1=\sqrt{3}\left(c{m}^2\right)$.

Xem thêm các bài giải SBT Toán 8 Cánh diều hay, chi tiết khác:

Bài 3: Hình thang cân

Bài 4: Hình bình hành

Bài 5: Hình chữ nhật

Bài 6: Hình thoi

Bài 7: Hình vuông

Bài tập cuối chương 5 trang 103