Giải SBT Toán 8 Bài 6: Hình thoi
Lời giải:
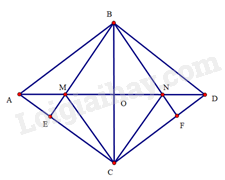
Gọi O là giao điểm của AC và BD
Do ABCD là hình thoi nên AC vuông góc với BD tại trung điểm O của BD. Suy ra AC là đường trung trực của BD. Do đó BM=DM,BN=DN.
Do ABCD là hình thoi nên BA=BC,^BAE=^BCF.
Suy ra ΔABE=ΔBCF (cạnh huyền – góc nhọn kề)
Do đó ^ABE=^CBF. Mà ^ABD=^CBD, suy ra ^MBO=^NBO.
ΔMBO=ΔNBO (cạnh góc vuông – góc nhọn). suy ra BM=BN
Mà BM=DM và BN=DN, suy ra BM=DM=BN=DN.
Tứ giác BMDN có BM=DM=BN=DN nên BMDN là hình thoi.
Lời giải:
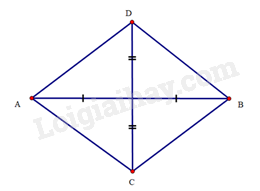
Xét hình thoi ABCD có AC=185m, BD=2710m.
Gọi O là giao điểm của hai đường chéo AC và BD.
Do ABCD là hình thoi nên AC⊥BD,O là trung điểm của AC và BD.
Ta tính được:
OA=AC2=95m
OB=BD2=2720m.
Trong tam giác OAB vuông tại O, ta có: AB2=OA2+OB2. Suy ra AB=94m
Chu vi của hình thoi ABCD là: 4.94=9(m)
Diện tích của hình thoi ABCD là: 12.185.2710=24350(m2).
a) BN⊥CM
b) Tứ giác MNHK là hình thoi.
Lời giải:
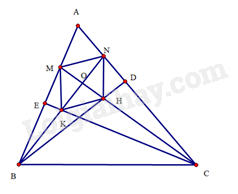
a) Do tam giác ABD vuông tại D và tam giác ACE vuông tại E nên ^ABD+ˆA=^ACE+ˆA=90∘. Suy ra ^ABD=^ACE.
Mà BN và CM lần lượt là tia phân giác của ^ABD và ^ACE, suy ra ^ABN=^DBN=^ACM=^ECM.
Do tam giác CEM vuông tại E nên ^ECM+^EMC=90∘
Suy ra ^ABN+^EMC=90∘ hay ^MBO+^BMO=90∘.
Do đó ta tính được ^BOM=90∘. Vậy BN⊥CM.
b) ΔBMO=ΔBHO (cạnh góc vuông – góc nhọn kề). Suy ra OM=OH
ΔCNO=ΔCKO (cạnh góc vuông – góc nhọn kề). Suy ra ON=OK.
Tứ giác MNHK có hai đường chéo MH và NK cắt nhau tại trung điểm O của mỗi đường nên MNHK là hình bình hành.
Hình bình hành MNHK có MH⊥NK nên MNHK là hình thoi.
Lời giải:
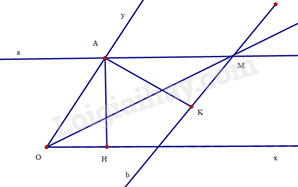
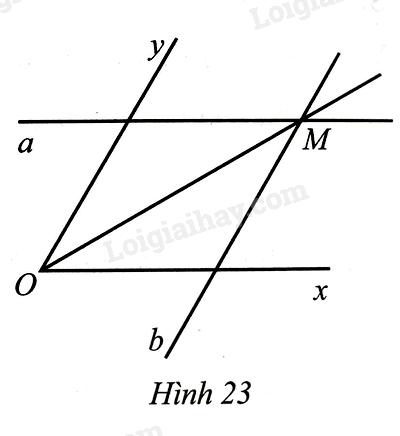
Gọi A là giao điểm của đường thẳng a với tia Oy, B là giao điểm của đường thẳng b với tia Ox. Kẻ AH vuông góc với OB tại H,AK vuông góc với BM tại K. Do khoảng cách giữa hai lề của thước là không đổi nên ta có AH=AK.
Tứ giác OAMB có AM//OB,MB//OA nên OAMB là hình bình hành. Suy ra ^AOH=^AMK. Do đó ^OAH=^MAK.
ΔAOH=ΔAMK (cạnh góc vuông – góc nhọn kề). Suy ra OA=AM.
Hình bình hành OAMB có OA=AM nên OAMB là hình thoi. Vậy OM là tia phân giác của góc xOy.
a) Chứng minh DH+DK không đổi
b) Xác định vị trí của các điểm H,K để độ dài HK ngắn nhất. Tính độ dài ngắn nhất đó.
Lời giải:
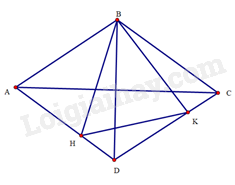
a) Do ABCD là hình thoi nên AB=DA=2cm,^ABD=^CDB=12^ABC
Mà ^BAD=12^ABC, suy ra ^BAD=^ABD. Do đó tam giác ABD cân tại D. Suy ra DA=DB.
Mà AB=DA, suy ra AB=DA=DB.
ΔABH=ΔDBK (g.c.g). Suy ra AH=DK. Do đó DH+DK=DH+AH=AD.
Vậy DH+DK không đổi
b) Do ΔABH=ΔDBk nên BH=BK.
Tam giác BHK có BH=BK và ^HBK=60∘ nên tam giác BHK là tam giác đều.
Suy ra HK=BH=BK.
Do đó, độ dài HK ngắn nhất khi BH và BK ngắn nhất. Vậy H,K lần lượt là hình chiếu của B trên AD,CD.
Khi đó ΔABH=ΔDBH (cạnh huyền – cạnh góc vuông)
Suy ra AH=DH=AD2=1cm
Trong tam giác ABH vuông tại H, ta có: AB2=AH2+BH2. Suy ra ta tính được BH=√3cm. Vậy độ dài ngắn nhất của HK là √3 cm.
Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác:




