Giải SBT Toán 8 Bài 7: Hình vuông
a) Chứng minh các tứ giác BOCF và BDKE đều là hình vuông.
b) Tứ giác CDOF có thể là hình vuông không? Vì sao?
Lời giải:
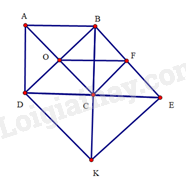
a) Tứ giác ABCD là hình vuông suy ra ^ACB=45∘,OB=OC,^BOC=^DOC=90∘.
Ta có: ^BOF=^DOC (hai góc đồng vị) nên ^OBF=90∘;^CBE=^ACB (hai góc so le trong) nên ^CBE=45∘.
Từ đó ta chứng minh được tam giác BDE vuông cân tại B và tam giác BCE vuông cân tại C. Suy ra BD=BE và BC=EC.
ΔBCF=ΔECF (c.c.c). Suy ra ta tính được ^BFC=^EFC=90∘
Tứ giác BOCF có ^BOC=^OBF=^BFC=90∘ nên BOCF là hình chữ nhật.
Hình chữ nhật BOCF có OB=OC nên BOCF là hình vuông.
Ta có: BC=CD và BC=CE nên CD=CE.
Tứ giác BDKE có hai đường chéo BK và DE cắt nhau tại trung điểm C của mỗi đường nên BDKE là hình bình hành.
Hình bình hành BDKE có ^DBE=90∘nên BDKE là hình chữ nhật
Hình chữ nhật BDKE có BD=BE nên BDKE là hình vuông
b) Tứ giác CDOF có ^ODC=45∘ nên CDOF không thể là hình vuông.
a) GH//CD
b) Tứ giác GFHE là hình vuông
Lời giải:
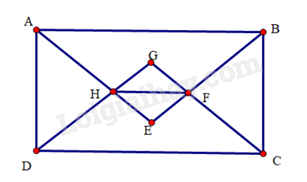
a) Do ABCD là hình chữ nhật nên ^DAB=^ABC=^BCD=^CDA=90∘
Mà AE,BE,CF,DF lần lượt là các tia phân giác của các góc DAB,ABC,BCD,CDA
suy ra ^DAE=^EAB=^ABE=^EBC=^BCF=^FCD=^CDF=^FDA=45∘
Do đó, các tam giác EAB,FCD,GAD,HBC đều là tam giác vuông cân.
ΔGAD=ΔHBC (g.c.g). Suy ra GD=HC. Mà FD=FC, suy ra FG=FH.
Do đó, tam giác FGH vuông cân tại F. Suy ra ^FGH=45∘.
Ta có: ^FGH=^CDF=45∘ và ^FGH,^CDF nằm ở vị trí đồng vị nên GH//CD.
b) ^EGF=^AGD=90∘ (hai góc đối đỉnh)
Tứ giác GFHE là hình chữ nhật.
Hình chữ nhật GFHE có FG=FH nên GFHE là hình vuông.
a) ΔAHF=ΔADC
b) AC⊥HF.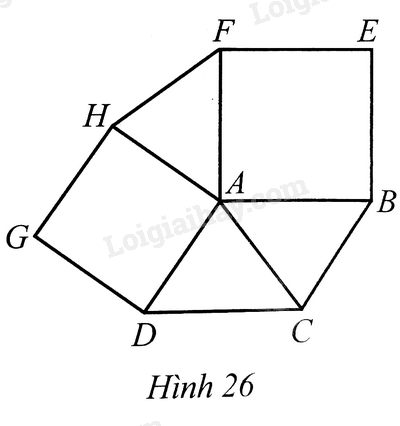
Lời giải:
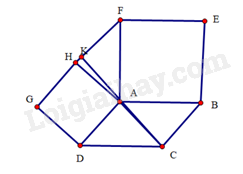
Gọi K là giao điểm của AC và HF
a) Do ABEF và ADGH đều là hình vuông nên^BAF=^DAH=90∘,AH=BA,AH=DA
Do ABCD là hình bình hành nên BA=DC. Suy ra AF=DC
Ta chứng minh được ^HAF+^DAB=180∘ và ^ADC+^DAB=180∘
Suy ra ^HAF=^ADC
Xét hai tam giác HAF và ADC, ta có: AH=DA,^HAF=^ADC,AF=DA
Suy ra ΔHAF=ΔADC (c.g.c)
b) Ta có: ^HAK+^DAH+^DAC=^CAK=180∘ và ^DAH=90∘ nên ^HAK+^DAC=90∘
Mà ^AHF=^DAC (vì ΔHAF=ΔADC), suy ra ^HAK+^AHF=90∘
Trong tam giác AHK, ta có: ^AKH+^HAK+^AHF=180∘. Suy ra ^AKH=90∘
Vậy AK⊥HK hai AC⊥HF.
a) Tứ giác EFHD là hình gì? Vì sao?
b) Tìm điều kiện của tam giác ABC để tứ giác EFHD là hình vuông.
Lời giải:
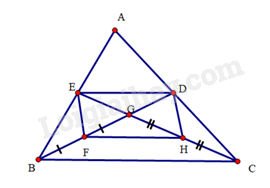
a) Do G là trọng tâm tam giác ABC nên DG=12BG,EG=12CG. Mà F,H lần lượt là trung điểm của BG,CG nên DG=BF=FG,EG=CH=HG.
Tứ giác EFHG có hai đường chéo EH và DF cắt nhau tại trung điểm của mỗi đường nên EFHG là hình bình hành.
b) Để hình bình hành EFHG là hình vuông thì EH=DF và EH⊥DF
suy ra BG=CG,EG=DG và BD⊥CE.
ΔBEG=ΔCDG (c.g.c). Suy ra BE=CD. Mà AB=2BE,AC=2CD, suy ra AB=AC.
Dễ thấy nếu AB=AC và BD⊥CE thì tứ giác EFHG là hình vuông.
Vậy tam giác ABC cân tại A có đường trung tuyến BD, CE vuông góc với nhau thì tứ giác EFHG là hình vuông.
a) Chứng minh AE=AM=DE
b) Tính độ dài BF.
Lời giải:
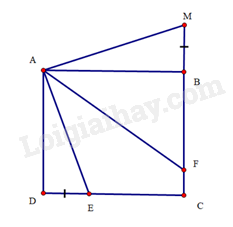
a) ΔADE=ΔABM(c.g.c)
Suy ra AE=AM và ^DAE=^BAM.
Do AF là tia phân giác của ^BAE nên ^EAF=^BAF.
Suy ra ^DAE+^EAF=^BAM+^BAF hay ^DAF=^MAF.
Mà ^DAF=^MFA (hai góc so le trong) , suy ra ^MFA=^MAF
Do đó, tam giác MAF cân tại M. Suy ra AM=FM
Mà AE=AM, suy ra AE=AM=FM.
b) Trong tam giác ADE vuông tại D, ta có: AE2=AD2+DE2
Suy ra AE=13cm. Mà FM=AE, suy ra FM=13cm.
Ta có: FM=BM+BF. Mà BM=DE=5cm và FM=13cm, suy ra BF=8cm.
a) Chứng minh tam giác AEF là tam giác vuông cân
b) Gọi I là trung điểm của EF. Trên tia đối của tia IA lấy điểm K sao cho IK=IA. Chứng minh tứ giác AEKF là hình vuông.
c) Chứng minh I thuộc đường thẳng BD.
Lời giải:
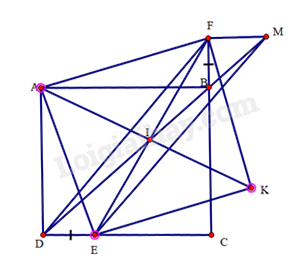
Từ điểm F kẻ đường thẳng song song với CD cắt đường thẳng BD tại M
a) ΔADE=ΔABF (c.g.c)
Suy ra AE=AF và ^DAE=^BAF
Suy ra ^DAE+^BAE=^BAF+^BAE hay ^BAD=^EAF.
Do đó, ^EAF=90∘
Tam giác AEF có ^EAF=90∘,AE=AF nên tam giac AEF vuông cân tại A.
b) Tứ giác AEKF có hai đường chéo AK,EF cắt nhau tại trung điểm I của mỗi đường nên AEKF là hình bình hành
hình bình hành AEKF có ^EAF=90∘ nên AEKF là hình chữ nhật.
hình chữ nhật AEKF có AE=AF nên AEKF là hình vuông.
c) Do ABCD là hình vuông nên ta tính được ^CBD=45∘. Mà ^FBM=^CBD (hai góc đối đỉnh), suy ra ^FBM=45∘.
Do MF=CD nên ^BFM=^BCD (cặp góc so le trong)
Do đó ^BFM=90∘. Ta chứng minh được tam giác null vuông cân tại F. Suy ra MF=BF. Mà BF=DE, suy ra MF=DE.
Tứ giác DEMF có MF=DE và MF//DE nên DEMF là hình bình hành.
Mà I là trung điểm của EF, suy ra I là trung điểm của DM
Vậy I thuộc đường thẳng DM hay I thuộc đường thẳng BD.
Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác:
Bài tập cuối chương 5 trang 103




