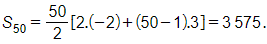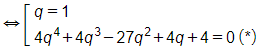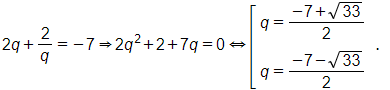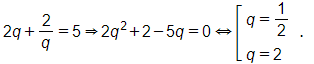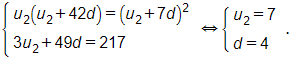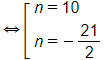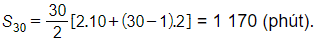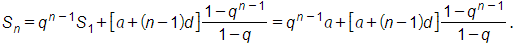Giải SBT Toán 11 (Kết nối tri thức) Bài tập cuối chương 2 trang 40

Giải SBT Toán lớp 11 Bài tập cuối chương 2 trang 40

A. TRẮC NGHIỆM

Bài 2.31 trang 40 SBT Toán 11 Tập 1: Cho dãy số (u_n) xác định bởi: u₁ = 1, u_{n + 1} = u_n + n. Số hạng u₄ là

A. 5.

B. 6.

C. 7.

D. 10.

Lời giải:

Đáp án đúng là: C

Ta có u₁ = 1;

u₂ = u₁ + 1 = 1 + 1 = 2;

u₃ = u₂ + 2 = 2 + 2 = 4;

u₄ = u₃ + 3 = 4 + 3 = 7.

Bài 2.32 trang 40 SBT Toán 11 Tập 1: Hãy chọn dãy số bị chặn trong các dãy số (u_n) sau:

A. u_n = 1 – n².

B. u_n = 2ⁿ.

C. u_n = n sin n.

D. $u_n=\frac{2-n}{n+1}$.

Lời giải:

Đáp án đúng là: D

Xét từng đáp án, ta thấy dãy số ở đáp án D là dãy số bị chặn. Thật vậy:

Ta có $u_n=\frac{2-n}{n+1}=\frac{-\left(n+1\right)+3}{n+1}=-1+\frac{3}{n+1}$.

Vì n > 0 nên $\frac{3}{n+1}>0$. Suy ra $-1+\frac{3}{n+1}>-1$.

Vì n ≥ 1 nên n + 1 ≥ 2 $\Rightarrow \frac{3}{n+1}\le \frac{3}{2}\Rightarrow -1+\frac{3}{n+1}\le \frac{1}{2}$

Vậy $-1<u_n\le \frac{1}{2}$ nên dãy số này bị chặn.

Bài 2.33 trang 41 SBT Toán 11 Tập 1: Hãy chọn dãy số tăng trong các dãy số (u_n) sau:

A. u_n = – 2n + 1.

B. u_n = n² – n + 1.

C.u_n = (– 1)ⁿ 2ⁿ.

D. u_n = 1 + sin n.

Lời giải:

Đáp án đúng là: B

Xét từng đáp án, ta thấy dãy số ở đáp án B là dãy số tăng. Thật vậy:

Ta có u_{n + 1} – u_n = [(n + 1)² – (n + 1) + 1] – (n² – n + 1)

                   = n² + 2n + 1 – n – 1 + 1 – n² + n – 1 = 2n > 0 với mọi n ≥ 1.

Tức là u_{n + 1} > u_n với mọi n ≥ 1. Vậy đây là dãy số tăng.

Bài 2.34 trang 41 SBT Toán 11 Tập 1: Cho dãy số $u_n=2020\sin \frac{n\pi }{2}+2021\cos \frac{n\pi }{3}$. Mệnh nào dưới đây là đúng?

A. u_{n + 6} = u_n.

B. u_{n + 9} = u_n.

C. u_{n + 4} = u_n.

D. u_{n + 12} = u_n.

Lời giải:

Đáp án đúng là: D

Ta có $u_{n+12}=2020\sin \frac{\left(n+12\right)\pi }{2}+2021\cos \frac{\left(n+12\right)\pi }{3}$

          $=2020\sin \left(\frac{n\pi }{2}+6\pi \right)+2021\cos \left(\frac{n\pi }{3}+4\pi \right)$

          $=2020\sin \frac{n\pi }{2}+2021\cos \frac{n\pi }{3}=u_n$ với mọi n.

Vậy u_{n + 12} = u_n.

Bài 2.35 trang 41 SBT Toán 11 Tập 1: Chọn cấp số cộng trong các dãy số (u_n) sau:

A. u_n = 3ⁿ + 2.

B. u_n = $\frac{3}{n}$ + 1.

C. u_n = 3n.

D. u₁ = 1, u_{n + 1} = u_n + n.

Lời giải:

Đáp án đúng là: C

Ta có dãy số (u_n) với u_n = 3n là cấp số cộng.

Thật vậy, u_{n + 1} – u_n = 3(n + 1) – 3n = 3 không đổi với mọi n.

Vậy dãy số này là cấp số cộng với công sai d = 3.

Bài 2.36 trang 41 SBT Toán 11 Tập 1: Cho cấp số cộng với u₁ = −2, u₉ = 22.Tổng của 50 số hạng đầu của cấp số cộng này là

A. 3 570.

B. 3 575.

C. 3 576.

D. 3 580.

Lời giải:

Đáp án đúng là: B

Ta có u₉ = u₁ + 8d = – 2 + 8d = 22. Suy ra d = 3.

Vậy tổng 50 số hạng đầu của cấp số cộng này là

Bài 2.37 trang 41 SBT Toán 11 Tập 1: Chọn cấp số nhân trong các dãy số (un) sau:

A. u_n = 2n.

B. $u_n=\frac{2}{n}$.

C. u_n = 2n.

D. u₁ = 1, u_n + 1 = nun.

Lời giải:

Đáp án đúng là: C

Ta có dãy số (un) với un = 2n là cấp số nhân.

Thật vậy, $\frac{u_{n+1}}{u_n}=\frac{2^{n+1}}{2^n}=2$ không đổi với mọi n.

Vậy dãy số này là cấp số nhân với công bội q = 2.

Bài 2.38 trang 41 SBT Toán 11 Tập 1: Tổng $1+\frac{1}{2}+\frac{1}{2^2}+\mathrm{...}+\frac{1}{2^n}$ bằng

A. $2+\frac{1}{2^n}$

B. $2-\frac{1}{2^{n-1}}$.

C. $2-\frac{1}{2^{n+1}}$.

D. $2-\frac{1}{2^n}$.

Lời giải:

Đáp án đúng là: D

Ta có $1+\frac{1}{2}+\frac{1}{2^2}+\mathrm{...}+\frac{1}{2^n}$. Nhận thấy các số hạng trong tổng này lập thành một cấp số nhân gồm n + 1 số hạng với số hạng đầu u₁ = 1 và công bội $q=\frac{1}{2}$.

Do đó $1+\frac{1}{2}+\frac{1}{2^2}+\mathrm{...}+\frac{1}{2^n}=u_1.\frac{1-q^{n+1}}{1-q}=1.\frac{1-{\left(\frac{1}{2}\right)}^{n+1}}{1-\frac{1}{2}}=2-\frac{1}{2^n}$.

Bài 2.39 trang 41 SBT Toán 11 Tập 1: Có bao nhiêu cấp số nhân có năm số hạng mà tổng của năm số hạng đó là 31 và tích của chúng là 1 024?

A. 1.

B. 2.

C. 3.

D. 4.

Lời giải:

Đáp án đúng là: D

Giả sử 5 số hạng của cấp số nhân đó là u₁; u₂; u₃; u₄; u₅ và công bội của cấp số nhân là q.

+ Nếu q = 0 thì tích các số hạng bằng 0 không thỏa mãn bài toán nên q ≠ 0.

+ Nếu q = 1 thì u₁ = u₂ = u₃ = u₄ = u₅, do đó u₁ + u₂ + u₃ + u₄ + u₅ = 5u₁ = 31.

Suy ra u₁ = u₂ = u₃ = u₄ = u₅ = $\frac{31}{5}$. Khi đó u₁ . u₂ . u₃ . u₄ . u₅ = ${\left(\frac{31}{5}\right)}^5\ne 1024$. Vô lí.

Vậy q ≠ 1.

+ Với q ≠ {0; 1}. Khi đó u₂ = u₁q; u₃ = u₁q²; u₄ = u₁q³; u₅ = u₁q⁴.

Ta có u₁ . u₂ . u₃ . u₄ . u₅ = $u_1^5.q^{1+2+3+4}=u_1^5{q}^{10}={\left(u_1{q}^2\right)}^5$ = 1 024 = 4⁵. Suy ra u₁q² = 4. 

Suy ra $u_1=\frac{4}{q^2}$.

Lại có u₁ + u₂ + u₃ + u₄ + u₅ = S₅ = $\frac{u_1\left(1-q^5\right)}{1-q}=\frac{\frac{4}{q^2}\left(1-q^5\right)}{1-q}=31$.

Suy ra 4(1 – q⁵) = 31q²(1 – q)

⇔ 4(1 – q)(1 + q + q² + q³ + q⁴) – 31q²(1 – q) = 0

⇔ (1 – q) (4 + 4q + 4q² + 4q³ + 4q⁴ – 31q²) = 0

⇔ (1 – q)(4q⁴ + 4q³ – 27q² + 4q + 4) = 0

Vì q ≠ 1 nên ta loại trường hợp q = 1.

Giải phương trình (*): Chia cả hai vế của (*) cho q² (do q ≠ 0) ta được

$4q^2+4q-27+\frac{4}{q}+\frac{4}{q^2}=0$

$\iff \left(4q^2+8+\frac{4}{q^2}\right)+\left(4q+\frac{4}{q}\right)-35=0$

$\iff {\left(2q+\frac{2}{q}\right)}^2+2\left(2q+\frac{2}{q}\right)-35=0$ (**)

Đặt $2q+\frac{2}{q}=t$, khi đó (**) ⇔ t² + 2t – 35 = 0 ⇔ t = – 7 hoặc t = 5.

+ Với t = – 7, ta có 

+ Với t = 5, ta có 

Thử lại ta thấy cả 4 giá trị của q đều thỏa mãn (*).

Vậy có 4 cấp số nhân có năm số hạng mà tổng của năm số hạng đó là 31 và tích của chúng là 1 024.

Bài 2.40 trang 41 SBT Toán 11 Tập 1: Ông Trung có 100 triệu đồng gửi tiết kiệm vào ngân hàng theo thể thức lãi kép kì hạn 6 tháng với lãi suất 8% một năm. Giả sử lãi suất không thay đổi. Hỏi sau 3 năm số tiền trong tài khoản tiết kiệm của ông Trung gần nhất với số nào sau đây?

A. 126 532 000 đồng.

B. 158 687 000 đồng.

C. 125 971 000 đồng.

D. 112 486 000 đồng.

Lời giải:

Đáp án đúng là: B

Ta có 100 triệu đồng = 100 000 000 đồng.

3 năm tương ứng với 6 kì lãi.

Vậy sau ba năm, số tiền trong tài khoản tiết kiệm của ông Trung là

S = 100 000 000 . (1 + 8%)⁶ ≈ 158 687 432 (đồng).

Xét các đáp án ta thấy 158 687 432 đồng gần nhất với 158 687 000 đồng.

Bài 2.41 trang 41 SBT Toán 11 Tập 1: Một du khách vào trường đua ngựa xem đua ngựa và đặt cược chọn con thắng cuộc. Nếu chọn đúng con thắng cuộc thì sẽ nhận được số tiền gấp đôi số tiền đặt cược, còn nếu chọn sai thì sẽ mất số tiền đặt cược. Người du khách đó lần đầu tiên đặt 20 000 đồng, mỗi lần sau tiền đặt gấp đôi tiền đặt lần trước. Người đó thua 9 lần liên tiếp và thắng ở lần thứ 10. Hỏi du khách đó thắng hay thua bao nhiêu?

A. Thắng 20 000 đồng.

B. Hoà vốn.

C. Thua 20 000 đồng.

D. Thua 40 000 đồng.

Lời giải:

Đáp án đúng là: A

Du khách đó lần đầu tiên đặt 20 000 đồng, mỗi lần sau tiền đặt gấp đôi tiền đặt lần trước.

Khi đó, số tiền đặt cược của du khách ở mỗi lần khác nhau lập thành một cấp số nhân với số hạng đầu là u₁ = 20 000 và công bội q = 2.

Người đó thua 9 lần liên tiếp nên tổng số tiền người đó đã bỏ ra và mất trong 9 lần đầu là:

$S_9=u_1\frac{1-q^9}{1-q}=20000.\frac{1-2^9}{1-2}=10220000$ (đồng).

Số tiền người đó bỏ ra ở lần thứ 10 là:

u₁₀ = u₁ . q^{10 – 1} = 20 000 . 2^{10 – 1} = 10 240 000 (đồng).

Vì người du khách đó thắng ở lần thứ 10. Người đó nhận bỏ ra và nhận lại gấp đôi, nghĩa là người đó lãi được: 10 240 000 (đồng).

Vậy thì sau 10 lần chơi, người đó đã thắng 20 000 đồng.

Bài 2.42 trang 42 SBT Toán 11 Tập 1: Ba số phân biệt có tổng là 217 có thể coi là các số hạng liên tiếp của một cấp số nhân, cũng có thể coi là số hạng thứ 2, thứ 9, thứ 44 của một cấp số cộng. Hỏi phải lấy bao nhiêu số hạng đầu của cấp số cộng này để tổng của chúng bằng 210?

A. 40.

B. 30.

C. 20.

D. 10.

Lời giải:

Đáp án đúng là: D

Gọi số hạng thứ 2, thứ 9 và thứ 44 của cấp số cộng này là u₂, u₉, u₄₄. Giả sử cấp số cộng có số hạng đầu là u₁ và công sai là d. Khi đó ta có:

u₂ = u₁ + d;

u₉ = u₁ + 8d = (u₁ + d) + 7d = u₂ + 7d;

 u₄₄ = u₁ + 43d = (u₁ + d) + 42d = u₂ + 42d.

Vì 3 số này là các số hạng liên tiếp của một cấp số nhân nên ta có: 

$u_2{u}_{44}=u_9^2$ hay u₂(u₂ + 42d) = (u₂ + 7d)².

Và tổng của 3 số đó là 217 nên u₂ + u₉ + u₄₄ = u₂ + u₂ + 7d + u₂ + 42d = 3u₂ + 49d = 217.

Vậy ta có hệ 

Do đó u₁ = u₂ – d = 7 – 4 = 3.

Gọi n số hạng đầu của cấp số cộng có tổng là 210.

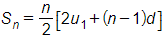
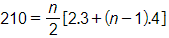
Khi đó  hay  ⇔ 210 = n(2n + 1)

⇔ 2n² + n – 210 = 0 

Vì n nguyên dương nên n = 10. Vậy phải lấy 10 số hạng đầu của cấp số cộng này để tổng của chúng bằng 210.

B. TỰ LUẬN

Bài 2.43 trang 42 SBT Toán 11 Tập 1: Trong các dãy số (u_n) dưới đây, dãy số nào là cấp số cộng, dãy số nào là cấp số nhân? Nếu dãy số là cấp số cộng hoặc cấp số nhân, hãy xác định công sai hoặc công bội của nó.

a) u₁ = 2, u_{n + 1} = u_n + n;

b) u_n = 6n + 3;

c) u₁ = 1, u_{n + 1} = n ∙ u_n;

d) u_n = 3 . 5ⁿ.

Lời giải:

a) Từ hệ thức truy hồi ta có u₁ = 2; u₂ = u₁ + 1 = 2 + 1 = 3; u₃ = u₂ + 2 = 3 + 2 = 5.

Ta có 3 – 2 = 1; 5 – 3 = 2 nên u₂ – u₁ ≠ u₃ – u₂ và $\frac{3}{2}\ne \frac{5}{3}$ nên $\frac{u_2}{u_1}\ne \frac{u_3}{u_2}$.

Do vậy, dãy số đã cho không là cấp số cộng và cũng không là cấp số nhân.

b) Từ u_n = 6n + 3, suy ra u_{n + 1} = 6(n + 1) + 3 = 6n + 9.

Ta có u_{n + 1} = (6n + 9) – (6n + 3) = 6 không đổi với mọi n ≥ 1.

Vậy dãy số đã cho là cấp số cộng với công sai d = 6.

c) Từ hệ thức truy hồi ta có u₁ = 1; u₂ = 1; u₃ = 2 . u₂ = 2.

Từ đó suy ra u₂ – u₁ ≠ u₃ – u₂ và $\frac{u_2}{u_1}\ne \frac{u_3}{u_2}$.

Vậy dãy số đã cho không là cấp số cộng và cũng không là cấp số nhân.

d) Từ u_n = 3 . 5ⁿ suy ra u_{n + 1} = 3 . 5^{n + 1} = 3 . 5 . 5ⁿ.

Ta có $\frac{u_{n+1}}{u_n}=\frac{{\mathrm{3.5.5}}^n}{{3.5}^n}=5$ không đổi với mọi n ≥ 1.

Vậy dãy số đã cho là cấp số nhân với công bội q = 5.

Bài 2.44 trang 42 SBT Toán 11 Tập 1: Chứng minh rằng:

a) Nếu a₁, a₂, a₃, ... và b₁, b₂, b₃, ... là hai cấp số cộng thì a₁ + b₁, a₂ + b₂, a₃ + b₃, ... cũng là cấp số cộng.

b) Nếu a₁, a₂, a₃, ... và b₁, b₂, b₃, ... là hai cấp số nhân thì a₁b₁, a₂b₂, a₃b₃, ... cũng là cấp số nhân.

Lời giải:

a) Theo giả thiết, ta giả sử dãy số (a_n) là cấp số cộng với công sai d₁ và dãy số (b_n) là cấp số cộng với công sai d₂ nên ta có:

a_{n + 1} = a_n + d₁ và b_{n + 1}  = b_n + d₂ với mọi n ≥ 1.

Khi đó a_{n + 1} + b_{n + 1} = (a_n + d₁) + (b_n + d₂) = (a_n + b_n) + d₁ + d₂ với mọi n ≥ 1.

Vậy dãy số (a_n + b_n) là cấp số cộng với công sai d₁ + d₂.

b) Theo giả thiết, ta giả sử dãy số (a_n) là cấp số nhân với công bội q₁ và dãy số (b_n) là cấp số nhân với công bội q₂ nên ta có:

q_{n + 1} = a_nq₁ và b_{n + 1}  = b_nq₂ với mọi n ≥ 1.

Khi đó a_{n + 1}b_{n + 1} = (a_nq₁) . (b_nq₂) = (a_nb_n)q₁q₂ với mọi n ≥ 1.

Vậy dãy số (a_nb_n) là cấp số nhân với công bội q₁q₂.

Bài 2.45 trang 42 SBT Toán 11 Tập 1: Một con chó con nặng 0,4 kg khi mới sinh và sau mỗi tuần tuổi khối lượng của nó tăng thêm 24%. Giả sử un (kg) là khối lượng của con chó vào cuối tuần tuổi thứ n.

a) Viết lần lượt các công thức tính u₂, u₃. Từ đó dự đoán công thức của u_n.

b) Con chó nặng bao nhiêu kilôgam khi được sáu tuần tuổi?

Lời giải:

a) Giả sử u_n (kg) là khối lượng của con chó vào cuối tuần tuổi thứ n.

Ta có u₁ = 0,4; u₂ = u₁ + u₁24% = u₁(1 + 0,24) = 1,24u₁;

u₃ = u₂ + u₂24% = u₂(1 + 0,24) = u₁(1 + 0,24)(1 + 0,24) = u₁(1 + 0,24)².

Cứ tiếp tục làm tương tự, ta dự đoán được công thức u_n = u₁(1 + 0,24)^{n – 1} với mọi n ≥ 1.

b) Sau sáu tuần tuổi thì con chó nặng là

u₆ = u₁(1 + 0,24)^{6 – 1} = 0,4 . (1,24)⁵ ≈ 1,173 (kg).

Bài 2.46 trang 42 SBT Toán 11 Tập 1: Bác Hưng quyết định tham gia một chương trình bơi lội để duy trì sức khoẻ. Bác bắt đầu bằng cách bơi 10 phút vào ngày đầu tiên, sau đó thêm 2 phút mỗi ngày sau đó.

a) Tìm công thức truy hồi cho số phút T_n mà bác ấy bơi vào ngày thứ n của chương trình.

b) Tìm sáu số hạng đầu của dãy số T_n.

c) Tìm công thức tổng quát của dãy số (T_n).

d) Bác Hưng đạt được mục tiêu bơi ít nhất 60 phút mỗi ngày vào ngày thứ bao nhiêu của chương trình?

e) Tính tổng thời gian bác Hưng bơi sau 30 ngày đầu của chương trình.

Lời giải:

Gọi T_n là số phút mà bác Hưng bơi vào ngày thứ n của chương trình.

a) Do bác bắt đầu bằng cách bơi 10 phút vào ngày đầu tiên, sau đó thêm 2 phút mỗi ngày sau đó nên ta có hệ thức truy hồi sau T₁ = 10, T_{n + 1} = T_n + 2 ∀ n ≥ 1.

b) Sáu số hạng đầu của dãy số là

T₁ = 10;

T₂ = T₁ + 2 = 10 + 2 = 12;

T₃ = T₂ + 2 = 12 + 2 = 14:

T₄ = T₃ + 2 = 14 + 2 = 16;

T₅ = T₄ + 2 = 16 + 2 = 18;

T₆ = T₅ + 2 = 18 + 2 = 20.

c) Từ công thức truy hồi T_{n + 1} = T_n + 2 suy ra T_{n + 1} – T_n = 2 không đổi ∀ n ≥ 1.

Do đó, dãy số (T_n) là cấp số cộng có số hạng đầu T₁ = 10 và công sai d = 2.

Suy ra, công thức tổng quát của dãy số là

T_n = T₁ + (n − 1)d = 10 + (n – 1).2 = 8 + 2n   ∀ n ≥ 1.

d) Ta có T_n ≥ 60 ⇔ 8 + 2n ≥ 60 ⇔ n ≥ 26.

Vậy bác Hưng đạt được mục tiêu bơi ít nhất 60 phút mỗi ngày vào ngày thứ 26 của chương trình.

e) Tổng thời gian bác Hưng bơi trong 30 ngày đầu của chương trình là

Bài 2.47 trang 43 SBT Toán 11 Tập 1: Dãy các số chính phương sau đây không phải là cấp số cộng

1, 4, 9, 16, 25, 36, 49, 64, 81, ...

Tuy nhiên, chúng ta có thể lập một cấp số cộng liên quan bằng cách tìm hiệu của các số hạng liên tiếp của dãy số này.

a) Viết tám số hạng đầu của cấp số cộng liên quan được mô tả ở trên. Tìm công thức của số hạng thứ n của cấp số cộng này.

b) Mô tả bằng cách nào để chúng ta có thể lập được một cấp số cộng từ dãy các số lập phương sau đây:

1, 8, 27, 64, 125, 216, 343, 512, 729, ...

c) Viết bảy số hạng đầu của cấp số cộng ở trong phần b) và tìm số hạng thứ n của nó.

Lời giải:

a) Công thức số hạng thứ n của dãy các số chính phương đã cho là n² ∀ n ≥ 1.

Tám số hạng đầu của cấp số cộng (u_n) được mô tả là

u₁ = 4 – 1 = 3; u₂ = 9 – 4 = 5; u₃ = 16 – 9 = 7; u₄ = 25 – 16 = 9;

u₅ = 36 – 25 = 11; u₆ = 49 – 36 = 13; u₇ = 64 – 49 = 15; u₈ = 81 – 64 = 17.

Theo giả thiết chúng ta xét hiệu của hai số hạng liên tiếp, do đó số hạng thứ n của cấp số cộng này là hiệu của số hạng thứ n + 1 và số hạng thứ n của dãy các số chính phương nên

u_n = (n + 1)² – n² = 2n + 1 ∀ n ≥ 1.

Ta chứng minh được dãy số (u_n) là cấp số cộng với công sai d = 2.

b) Xét dãy các số lập phương, với ba số hạng liên tiếp ta lấy số đầu cộng với số thứ ba trừ đi 2 lần số thứ hai ta thu được một cấp số cộng.

c) Bảy số hạng đầu của cấp số cộng ở trong câu b là 12; 18; 24; 30; 36, 42, 48,

u₁ = 1 + 27 – 2 . 8 = 12;

u₂ = 8 + 64 – 2 . 27 = 18;

u₃ = 27 + 125 – 2 . 64 = 24;

u₄ = 64 + 216 – 2 . 125 = 30;

u₅ = 125 + 343 – 2 . 216 = 36;

u₆ = 216 + 512 – 2 . 343 = 42;

u₇ = 343 + 729 – 2 . 512 = 48.

Công thức số hạng thứ n của cấp số cộng này là

u_n = n³ + (n + 2)³ – 2(n + 1)³ = 6n + 6    ∀ n ≥ 1.

Bài 2.48 trang 43 SBT Toán 11 Tập 1: Chứng minh rằng nếu ba số theo thứ tự vừa lập thành một cấp số cộng vừa lập thành một cấp số nhân thì ba số ấy bằng nhau.

Lời giải:

Gọi x, y lần lượt là số thứ nhất và số thứ ba trong ba số đó. 

Vì ba số theo thứ tự đó lập thành một cấp số cộng nên số thứ hai là $\frac{x+y}{2}$

Khi đó, ba số cần tìm có dạng: x, $\frac{x+y}{2}$, y.

Vì ba số này lập thành một cấp số nhân nên ta có

$xy={\left(\frac{x+y}{2}\right)}^2$⇔ 4xy = x² + 2xy + y² ⇔ x² – 2xy + y² = 0 ⇔ (x − y)² = 0, tức là x = y.

Suy ra $\frac{x+y}{2}=\frac{x+x}{2}=\frac{2x}{2}=x$.

Vậy ba số đó bằng nhau.

Bài 2.49 trang 43 SBT Toán 11 Tập 1: Anh Nam là một cầu thủ bóng đá chuyên nghiệp. Anh vừa kí hợp đồng 5 năm với một câu lạc bộ với mức lương năm khởi điểm là 300 triệu đồng. Chủ tịch câu lạc bộ đưa ra cho anh Nam ba phương án về lương như sau:

- Phương án 1: Mỗi năm ngoài mức lương cố định như trên, sẽ được thưởng thêm 50 triệu đồng.

- Phương án 2: Mỗi năm lương sẽ tăng thêm 10% so với lương năm trước đó, bắt đầu kể từ năm thứ hai.

- Phương án 3: Mỗi năm lương sẽ tăng thêm 30 triệu so với lương năm trước đó, bắt đầu kể từ năm thứ hai.

Em hãy tính giúp anh Nam xem với phương án lương nào thì tổng lương sau 5 năm của anh Nam là lớn nhất?

Lời giải:

Ta tính tổng tiền lương của anh Nam theo từng phương án:

- Phương án 1: Mỗi năm ngoài mức lương cố định như trên, sẽ được thưởng thêm 50 triệu đồng thì sau 5 năm tổng số tiền lương của anh Nam là

5 . 300 + 5 . 50 = 1 750 (triệu đồng).

- Phương án 2: Mỗi năm lương sẽ tăng thêm 10% so với lương năm trước đó, bắt đầu kể từ năm thứ hai thì sau 5 năm tổng số tiền lương của anh Nam là

300 + 300 . (1 + 10%) + 300 . (1 + 10%)² + 300 . (1 + 10%)³ + 300 . (1 + 10%)⁴

= 1 831,53 (triệu đồng).

- Phương án 3: Mỗi năm lương sẽ tăng thêm 30 triệu so với lương năm trước đó, bắt đầu kể từ năm thứ hai thì sau 5 năm tổng số tiền lương của anh Nam là

300 + 330 + 360 + 390 + 420 = 1 800 (triệu đồng).

Vậy anh Nam nên sử dụng phương án 2 để nhận được tổng lương sau 5 năm là cao nhất.

Bài 2.50 trang 43 SBT Toán 11 Tập 1: Một dãy số (u_n) được gọi là một cấp số nhân cộng nếu nó cho bởi hệ thức truy hồi

u₁ = a, u_{n + 1} = qu_n + d.

Nếu q = 1 ta có cấp số cộng với công sai d, còn nếu d = 0 ta có cấp số nhân với công bội q.

a) Giả sử q ≠ 1. Dự đoán công thức số hạng tổng quát u_n.

b) Thiết lập công thức tính tổng S_n của n số hạng đầu của cấp số nhân cộng (u_n).

Lời giải:

a) Ta viết lần lượt các số hạng của dãy:

u₁ = a;

u₂ = qu₁ + d;

u₃ = qu₂ + d = q(qu₁ + d) + d = q²u₁ + qd + d = q²u₁+ d(q + 1);

u₄ = qu₃ + d = q(q²u₁ + qd + d) + d = q³u₁ + q²d + qd + d

= q³u₁ + d(q² + q + 1) = q³u₁ + d$\frac{1-q^3}{1-q}$     (với q ≠ 1).

Làm tương tự ta được công thức số hạng tổng quát u_n:

u_n = q^{n – 1}u₁ + d(q^{n – 2} + q^{n – 3} + ... + 1) = q^{n – 1}u₁ + d$\frac{1-q^{n-1}}{1-q}$.

b) Ta viết tổng n số hạng đầu như sau

S_n = u₁ + u₂ + ... + u_n

= u­₁ + (qu₁ + d) + (qu₂ + d) + ... + (qu_{n – 1} + d)

= u₁ + q(u₁ + u₂ + ... + u_{n – 1}) + (n – 1)d

= u₁ + qS_{n – 1} + (n – 1)d

= qS_{n – 1} + a + (n – 1)d               (vì u₁ = a).

Như vậy, ta được (S_n) cũng là một cấp số nhân cộng với S₁ = u₁ = a.

Áp dụng công thức số hạng tổng quát vừa tìm được ở câu a để tính S_n ta có

Vậy 

Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 6: Cấp số cộng

Bài 7: Cấp số nhân

Bài 8: Mẫu số liệu ghép nhóm

Bài 9: Các số đặc trưng đo xu thế trung tâm

Bài tập cuối chương 3