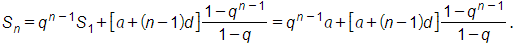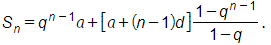Một dãy số (un) được gọi là một cấp số nhân cộng nếu nó cho bởi hệ thức truy hồi u1 = a

Bài 2.50 trang 43 SBT Toán 11 Tập 1: Một dãy số (u_n) được gọi là một cấp số nhân cộng nếu nó cho bởi hệ thức truy hồi

u₁ = a, u_{n + 1} = qu_n + d.

Nếu q = 1 ta có cấp số cộng với công sai d, còn nếu d = 0 ta có cấp số nhân với công bội q.

a) Giả sử q ≠ 1. Dự đoán công thức số hạng tổng quát u_n.

b) Thiết lập công thức tính tổng S_n của n số hạng đầu của cấp số nhân cộng (u_n).

Trả lời

a) Ta viết lần lượt các số hạng của dãy:

u₁ = a;

u₂ = qu₁ + d;

u₃ = qu₂ + d = q(qu₁ + d) + d = q²u₁ + qd + d = q²u₁+ d(q + 1);

u₄ = qu₃ + d = q(q²u₁ + qd + d) + d = q³u₁ + q²d + qd + d

= q³u₁ + d(q² + q + 1) = q³u₁ + d$\frac{1-q^3}{1-q}$     (với q ≠ 1).

Làm tương tự ta được công thức số hạng tổng quát u_n:

u_n = q^{n – 1}u₁ + d(q^{n – 2} + q^{n – 3} + ... + 1) = q^{n – 1}u₁ + d$\frac{1-q^{n-1}}{1-q}$.

b) Ta viết tổng n số hạng đầu như sau

S_n = u₁ + u₂ + ... + u_n

= u­₁ + (qu₁ + d) + (qu₂ + d) + ... + (qu_{n – 1} + d)

= u₁ + q(u₁ + u₂ + ... + u_{n – 1}) + (n – 1)d

= u₁ + qS_{n – 1} + (n – 1)d

= qS_{n – 1} + a + (n – 1)d               (vì u₁ = a).

Như vậy, ta được (S_n) cũng là một cấp số nhân cộng với S₁ = u₁ = a.

Áp dụng công thức số hạng tổng quát vừa tìm được ở câu a để tính S_n ta có

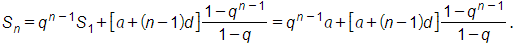
Vậy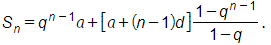 

Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 6: Cấp số cộng

Bài 7: Cấp số nhân

Bài tập cuối chương 2

Bài 8: Mẫu số liệu ghép nhóm

Bài 9: Các số đặc trưng đo xu thế trung tâm

Bài tập cuối chương 3