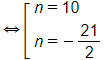Ba số phân biệt có tổng là 217 có thể coi là các số hạng liên tiếp của một cấp số nhân, cũng có
422
08/09/2023
Bài 2.42 trang 42 SBT Toán 11 Tập 1: Ba số phân biệt có tổng là 217 có thể coi là các số hạng liên tiếp của một cấp số nhân, cũng có thể coi là số hạng thứ 2, thứ 9, thứ 44 của một cấp số cộng. Hỏi phải lấy bao nhiêu số hạng đầu của cấp số cộng này để tổng của chúng bằng 210?
A. 40.
B. 30.
C. 20.
D. 10.
Trả lời
Đáp án đúng là: D
Gọi số hạng thứ 2, thứ 9 và thứ 44 của cấp số cộng này là u2, u9, u44. Giả sử cấp số cộng có số hạng đầu là u1 và công sai là d. Khi đó ta có:
u2 = u1 + d;
u9 = u1 + 8d = (u1 + d) + 7d = u2 + 7d;
u44 = u1 + 43d = (u1 + d) + 42d = u2 + 42d.
Vì 3 số này là các số hạng liên tiếp của một cấp số nhân nên ta có:
hay u2(u2 + 42d) = (u2 + 7d)2.
Và tổng của 3 số đó là 217 nên u2 + u9 + u44 = u2 + u2 + 7d + u2 + 42d = 3u2 + 49d = 217.
Vậy ta có hệ 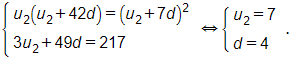
Do đó u1 = u2 – d = 7 – 4 = 3.
Gọi n số hạng đầu của cấp số cộng có tổng là 210.
Khi đó 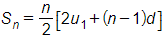 hay
hay 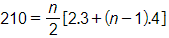 ⇔ 210 = n(2n + 1)
⇔ 210 = n(2n + 1)
⇔ 2n2 + n – 210 = 0 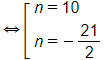
Vì n nguyên dương nên n = 10. Vậy phải lấy 10 số hạng đầu của cấp số cộng này để tổng của chúng bằng 210.
Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
Bài 6: Cấp số cộng
Bài 7: Cấp số nhân
Bài tập cuối chương 2
Bài 8: Mẫu số liệu ghép nhóm
Bài 9: Các số đặc trưng đo xu thế trung tâm
Bài tập cuối chương 3

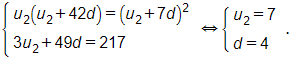
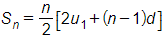 hay
hay 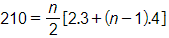 ⇔ 210 = n(2n + 1)
⇔ 210 = n(2n + 1)