Giải SBT Toán 11 (Kết nối tri thức) Bài 30: Công thức nhân xác suất cho hai biến cố độc lập

Sách bài tập Toán lớp 11 Bài 30: Công thức nhân xác suất cho hai biến cố độc lập

Bài 8.9 trang 51 SBT Toán 11 Tập 2: Cho P(A) = 0,4; P(B) = 0,5; P(A $\cup$ B) = 0,6. Hỏi A và B có độc lập hay không?

Lời giải:

Từ công thức cộng xác suất, suy ra

P(AB) = P(A) + P(B) – P(A $\cup$ B) = 0,4 + 0,5 – 0,6 = 0,3.

Lại có P(A) . P(B) = 0,4 ∙ 0,5 = 0,2.

Do đó, P(AB) ≠ P(A) . P(B).

Vậy A và B không độc lập.

Bài 8.10 trang 51 SBT Toán 11 Tập 2: Cho P(A) = $\frac{2}{5}$; P(B) = $\frac{1}{3}$; P(A$\cup$B) = $\frac{1}{2}$. Hỏi A và B có độc lập hay không?

Lời giải:

Từ công thức cộng xác suất, suy ra

P(AB) = P(A) + P(B) – P(A $\cup$ B) = $\frac{2}{5}+\frac{1}{3}-\frac{1}{2}=\frac{7}{30}$ .

Lại có P(A).P(B) = $\frac{2}{5}\cdot \frac{1}{3}=\frac{2}{15}=\frac{4}{30}$.

Do đó, P(AB) ≠ P(A) . P(B).

Vậy A và B không độc lập.

Bài 8.11 trang 51 SBT Toán 11 Tập 2: Gieo hai đồng xu cân đối. Xét các biến cố A: “Cả hai đồng xu đều ra mặt sấp”, B: “Có ít nhất một đồng xu ra mặt sấp”. Hỏi A và B có độc lập hay không?

Lời giải:

Ta có $\Omega$ = {SS; SN; NS; NN}, n($\Omega$) = 4.

A = {SS}, n(A) = 1. Do đó P(A) = $\frac{1}{4}$ .

B = {SS; SN; NS}, n(B) = 3. Do đó P(B) = $\frac{3}{4}$.

AB = A $\cap$ B = {SS}, n(AB) = 1. Do đó P(AB) = $\frac{1}{4}$ .

Vì P(AB) = $\frac{1}{4}$= $\frac{4}{16}$ $\ne$P(A).P(B) = $\frac{3}{16}$ nên A và B không độc lập.

Vậy A và B không độc lập.

Bài 8.12 trang 51 SBT Toán 11 Tập 2: Gieo hai con xúc xắc cân đối. Xét các biến cố A: “Có ít nhất một con xúc xắc xuất hiện mặt 5 chấm”, B: “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 7”. Chứng tỏ rằng A và B không độc lập.

Lời giải:

Vì gieo hai con xúc xắc cân đối nên ta có n($\Omega$) = 36.

Xét biến cố đối $\overline{A}$ : “Cả hai con xúc xắc không xuất hiện mặt 5 chấm”.

$\overline{A}$ = {(a,b):a,b$\in${1;2;3;4;6}}. Ta có n($\overline{A}$) = 25.

Do đó P($\overline{A}$) = $\frac{25}{36}$$\Rightarrow$P(A) = 1-P($\overline{A}$) = 1-$\frac{25}{36}$ = $\frac{11}{36}$.

Ta có B = {(1, 6); (2, 5); (3, 4); (4, 3); (5, 2); (6, 1)}, n(B) = 6.

Do đó P(B) = $\frac{6}{36}$ .

AB = A $\cap$ B = {(2, 5); (5, 2)}, n(AB) = 2. Do đó P(AB) = $\frac{2}{36}$ .

Vì P(AB) = $\frac{2}{36}$ = $\frac{72}{{36}^2}\ne$P(A).P(B) = $\frac{66}{{36}^2}$ nên A và B không độc lập.

Vậy A và B không độc lập.

Bài 8.13 trang 51 SBT Toán 11 Tập 2: Có 3 hộp I, II, III. Mỗi hộp chứa ba tấm thẻ đánh số 1, 2, 3. Từ mỗi hộp rút ngẫu nhiên một tấm thẻ. Xét các biến cố sau:

A: “Tổng các số ghi trên ba tấm thẻ là 6”; B: “Ba tấm thẻ có ghi số bằng nhau”.

a) Tính P(A), P(B).

b) Hỏi A, B có độc lập không?

Lời giải:

a) Ta có $\Omega$ = {(a, b, c): 1 ≤ a, b, c ≤ 3}, n($\Omega$) = 27.

A = {(1, 2, 3); (2, 1, 3); (3, 1, 2); (1, 3, 2); (3, 2, 1); (2, 3, 1); (2, 2, 2)}, n(A) = 7.

Do đó P(A) = $\frac{7}{27}$.

B = {(1, 1, 1); (2, 2, 2); (3, 3, 3)}, n(B) = 3. Do đó P(B) = $\frac{3}{27}=\frac{1}{9}$.

b) Có AB = A $\cap$ B = {(2, 2, 2)}, n(AB) = 1. Vậy P(AB) = $\frac{1}{27}$ .

Vì P(AB) = $\frac{1}{27}$ = $\frac{27}{{27}^2}$ $\ne$P(A).P(B) = $\frac{21}{{27}^2}$ nên A và B không độc lập.

Vậy A và B không độc lập.

Bài 8.14 trang 51 SBT Toán 11 Tập 2: Hai bạn An và Bình không quen biết nhau và đều học xa nhà. Xác suất để bạn An về thăm nhà vào ngày Chủ nhật là 0,2 và của bạn Bình là 0,25. Dùng sơ đồ hình cây để tính xác suất vào ngày Chủ nhật:

a) Cả hai bạn đều về thăm nhà.

b) Có ít nhất một bạn về thăm nhà.

c) Cả hai bạn đều không về thăm nhà.

d) Chỉ có bạn An về thăm nhà.

e) Có đúng một bạn về thăm nhà.

Lời giải:

Gọi A, B tương ứng là các biến cố: “Bạn An về thăm nhà vào ngày Chủ nhật” và “Bạn Bình về thăm nhà vào ngày Chủ nhật”. A và B là hai biến cố độc lập.

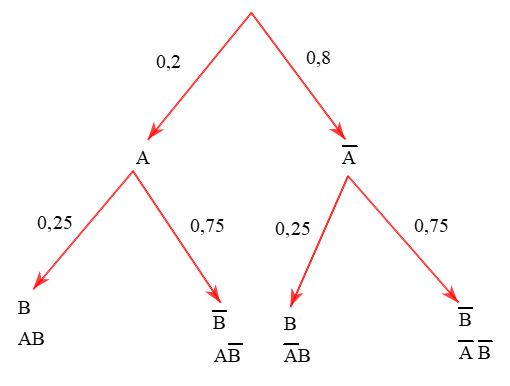
Ta có sơ đồ hình cây:

a) P(AB) = P(A) × P(B) = 0,2 × 0,25 = 0,05.

Vậy xác suất để cả hai bạn đều về thăm nhà là 0,05.

b) P(A $\cup$ B) = P(A) + P(B) – P(AB) = 0,2 + 0,25 – 0,05 = 0,4.

Vậy xác suất để có ít nhất một bạn về thăm nhà là 0,4.

c) P($\overline{A}$$\overline{B}$) = P($\overline{A}$).P($\overline{B}$) = 0,8.0,75 = 0,6.

Vậy xác suất để cả hai bạn đều không về thăm nhà là 0,6.

d) P($A\overline{B}$) = P(A).P($\overline{B}$) = 0,2.0,75 = 0,15.

Vậy xác suất để chỉ có bạn An về thăm nhà là 0,15.

e) $P\left(A\overline{B}\cup \overline{A}B\right)=$ $P\left(A\overline{B}\right)+P\left(\overline{A}B\right)$ = 0,2.0,75 + 0,8.0,25 = 0,35.

Vậy xác suất để có đúng một bạn về thăm nhà là 0,35.

Bài 8.15 trang 51 SBT Toán 11 Tập 2: Cho A, B là hai biến cố độc lập và P(AB) = 0,1; P($A\overline{B}$) = 0,4. Tìm P(A$\cup$$\overline{B}$).

Lời giải:

Theo công thức cộng xác suất ta có: P(A$\cup$$\overline{B}$) = P(A)+P($\overline{B}$) - P($A\overline{B}$).

Lại có A = AB$\cup$$A\overline{B}$, suy ra P(A) = P(AB) + P($A\overline{B}$) = 0,1+0,4 = 0,5.

Do A, B là hai biến cố độc lập nên P(AB) = P(A) . P(B) hay 0,1 = 0,5 . P(B)

⇒ P(B) = 0,2.

Vì P(B) = 0,2 nên P($\overline{B}$) = 1-P(B) = 1-0,2 = 0,8.

Do đó P(A$\cup$$\overline{B}$) = P(A) + P($\overline{B}$) - P($A\overline{B}$) = 0,5 + 0,8 – 0,4 = 0,9.

Vậy P(A$\cup$$\overline{B}$) = 0,9.

Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác: