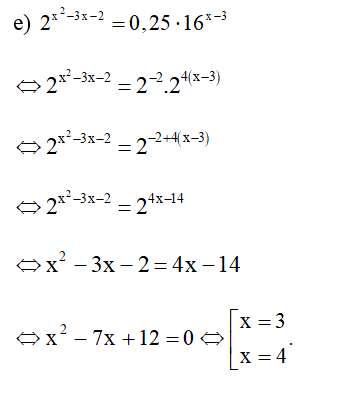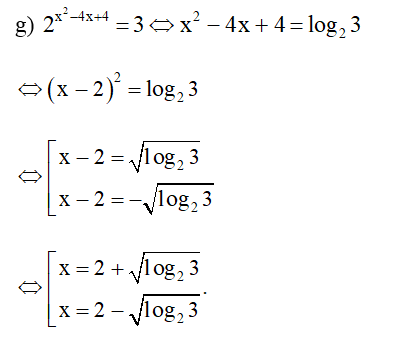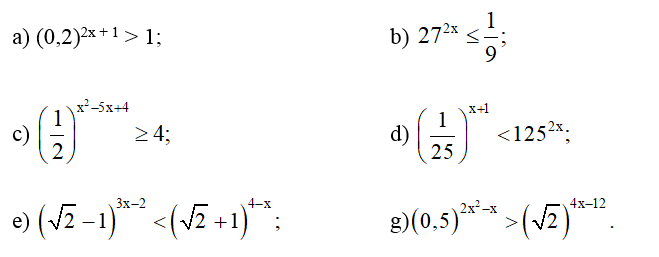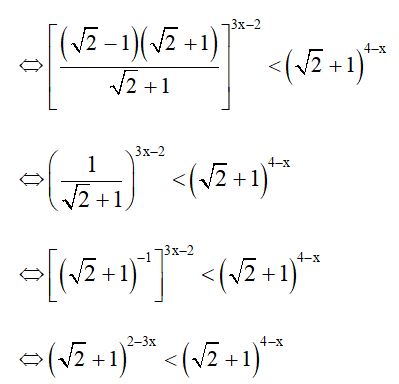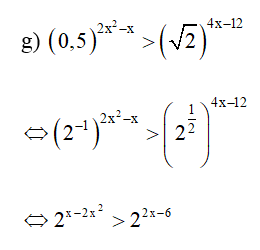Giải SBT Toán 11 (Cánh diều) Bài 4: Phương trình, bất phương trình mũ và lôgarit

Giải SBT Toán 11 Bài 4: Phương trình, bất phương trình mũ và lôgarit

Bài 53 trang 49 SBT Toán 11 Tập 2: Nghiệm của phương trình 2^{x – 1} = 8 là:

A. 2;

B. 4;

C. 3;

D. 5.

Lời giải:

Đáp án đúng là: B

Ta có: 2^{x – 1} = 8 ⇔ 2^{x – 1} = 2³ ⇔ x – 1 = 3 ⇔ x = 4.

Vậy phương trình có nghiệm là x = 4.

Bài 54 trang 50 SBT Toán 11 Tập 2: Nghiệm của phương trình 2^x = 5 là:

A.$x=\sqrt{5};$

B.$x=\frac{5}{2};$

C. x = log₂5;

D. x = log₅2.

Lời giải:

Đáp án đúng là: C

Ta có: 2^x = 5 ⇔ x = log₂5.

Vậy phương trình có nghiệm là x = log₂5.

Bài 55 trang 50 SBT Toán 11 Tập 2: Nghiệm của phương trình 9^{2x + 1} = 27^{x – 3} là:

A. x = – 9;

B. x = 11;

C. x = 9;

D. x = – 11.

Lời giải:

Đáp án đúng là: D

Ta có: 9^{2x + 1} = 27^{x – 3}

⇔ 3^{2(2x + 1)} = 3^{3(x – 3)}

⇔ 2(2x + 1) = 3(x – 3)

⇔ x = – 11.

Vậy phương trình có nghiệm là x = –11.

Bài 56 trang 50 SBT Toán 11 Tập 2: Nghiệm của phương trình log₂(x – 5) = 4 là:

A. x = 21;

B. x = 9;

C. x = 13;

D. x = 7.

Lời giải:

Đáp án đúng là: A

Ta có: log₂(x – 5) = 4 ⇔ x – 5 = 2⁴ ⇔ x – 5 = 16 ⇔ x = 21.

Vậy phương trình có nghiệm là x = 21.

Bài 57 trang 50 SBT Toán 11 Tập 2: Nghiệm của phương trình ${\log }_{\frac{1}{2}}\left(x-1\right)=-2$ là:

A. x = 2;

B. x = 5;

C. $x=\frac{5}{2};$

D. $x=\frac{3}{2}.$

Lời giải:

Đáp án đúng là: B

${\log }_{\frac{1}{2}}\left(x-1\right)=-2\iff x-1={\left(\frac{1}{2}\right)}^{-2}$

⇔ x – 1 = 4 ⇔ x = 5.

Vậy phương trình có nghiệm là x = 5.

Bài 58 trang 50 SBT Toán 11 Tập 2: Số nghiệm của phương trình log(x² – 7x + 12) = log(2x – 8) là:

A. 0;

B. 1;

C. 2;

D. 3.

Lời giải:

Đáp án đúng là: B

log(x² – 7x + 12) = log(2x – 8)

$\iff \left\{\begin{array}{l}{x}^2-7x+12=2x-8\\ 2x-8>0\end{array}\right.\iff \left\{\begin{array}{l}{x}^2-9x+20=0\\ x>4\end{array}\right.$

$\iff \left\{\begin{array}{l}\left[\begin{array}{l}x=4\\ x=5\end{array}\right.\\ x>4\end{array}\right.\iff x=5.$

Vậy phương trình có nghiệm x = 5.

Bài 59 trang 50 SBT Toán 11 Tập 2: Nghiệm của bất phương trình 2^x < 5 là:

A. x > log₂5;

B. x < log₅2;

C. x < log₂5;

D. x > log₅2.

Lời giải:

Đáp án đúng là: C

Ta có: 2^x < 5 ⇔ x < log₂5 (do 2 > 1)

Vậy tập nghiệm của bất phương trình là (–∞; log₂5).

Bài 60 trang 50 SBT Toán 11 Tập 2: Tập nghiệm của bất phương trình log_0,2(x + 1) > –3 là:

A. (–1; 124);

B. (124; +∞);

C. $\left(-1;-\frac{26}{27}\right);$

D. (–∞; 124).

Lời giải:

Đáp án đúng là: A

Do 0 < 0,2 < 1 nên ta có:

log_0,2 (x + 1) > –3

⇔ 0 < x + 1 < 0,2^–3

⇔ 0 < x + 1 < 125

⇔ –1 < x < 124.

Vậy tập nghiệm của bất phương trình (–1; 124).

Bài 61 trang 50 SBT Toán 11 Tập 2: Giải mỗi phương trình sau:

a) 3^{x – 1} = 5;

b) $3^{x^2-4x+5}=9;$

c) $2^{2x+3}=8\sqrt{2};$

d) 8^{x – 2} = 4^{1 – 2x};

e) $2^{x^2-3x-2}=0,25\cdot {16}^{x-3};$

g) $2^{x^2-4x+4}=3.$

Lời giải:

a) 3^{x – 1} = 5 ⇔ x – 1 = log₃5 ⇔ x = log₃5 + 1.

Vậy phương trình có nghiệm x = log₃5 + 1.

b) $3^{x^2-4x+5}=9\iff 3^{x^2-4x+5}=3^2\iff x^2-4x+5=2$

$\iff x^2-4x+3=0\iff \left[\begin{array}{l}x=1\\ x=3\end{array}\right..$

Vậy phương trình có nghiệm x ∈ {1; 3}.

c) $2^{2x+3}=8\sqrt{2}\iff 2^{2x+3}=2^3{.2}^{\frac{1}{2}}\iff 2^{2x+3}=2^{\frac{7}{2}}$

$\iff 2x+3=\frac{7}{2}\iff x=\frac{1}{4}.$

Vậy phương trình có nghiệm $x=\frac{1}{4}.$

d) 8^{x – 2} = 4^{1 – 2x} ⇔ 2^{3(x – 2)} = 2^{2(1 – 2x)}

⇔ 3(x – 2) = 2(1 – 2x) ⇔ 7x = 8

$\iff x=\frac{8}{7}.$

Vậy phương trình có nghiệm $x=\frac{8}{7}.$

Vậy phương trình có nghiệm x ∈ {3; 4}.

Vậy phương trình có nghiệm $x\in \left\{2+\sqrt{lo{g}_{2}3};2-\sqrt{lo{g}_{2}3}\right\}.$

Bài 62 trang 50 SBT Toán 11 Tập 2: Giải mỗi phương trình sau:

a) log₄ (x – 4) = –2;

b) log₃ (x² + 2x) = 1;

c) ${\log }_{25}\left(x^2-4\right)=\frac{1}{2};$

d) log₉ [(2x – 1)²] = 2;

e) log(x² – 2x) = log(2x – 3);

g) ${\log }_2\left(x^2\right)+{\log }_{\frac{1}{2}}\left(2x+8\right)=0.$

Lời giải:

a) log₄ (x – 4) = –2 ⇔ x – 4 = 4^–2

$\iff x-4=\frac{1}{16}\iff x=\frac{65}{16}.$

Vậy phương trình có nghiệm $x=\frac{65}{16}.$

b) log₃ (x² + 2x) = 1 ⇔ x² + 2x = 3¹

$\iff x^2+2x-3=0\iff \left[\begin{array}{l}x=-3\\ x=1\end{array}\right..$

Vậy phương trình có nghiệm x ∈ {– 3; 1}.

c) ${\log }_{25}\left(x^2-4\right)=\frac{1}{2}\iff x^2-4={25}^{\frac{1}{2}}$

$\iff x^2-4=5\iff x^2=9\iff \left[\begin{array}{l}x=3\\ x=-3\end{array}\right..$

Vậy phương trình có nghiệm x ∈ {– 3; 3}.

d) ${\log }_9\left[{\left(2x-1\right)}^2\right]=2\iff {\left(2x-1\right)}^2=9^2$

$\iff 4x^2-4x-80=0\iff \left[\begin{array}{l}x=-4\\ x=5\end{array}\right..$

Vậy phương trình có nghiệm x ∈ {– 4; 5}.

e) Ta có: $\log \left(x^2-2x\right)=\log \left(2x-3\right)$

$\iff \left\{\begin{array}{l}{x}^2-2x=2x-3\\ 2x-3>0\end{array}\right.\iff \left\{\begin{array}{l}{x}^2-4x+3=0\\ x>\frac{3}{2}\end{array}\right.$

$\iff \left\{\begin{array}{l}\left[\begin{array}{l}x=1\\ x=3\end{array}\right.\\ x>\frac{3}{2}\end{array}\right.\iff x=3.$

Vậy phương trình có nghiệm x = 3.

g) ${\log }_2\left(x^2\right)+{\log }_{\frac{1}{2}}\left(2x+8\right)=0.$

$\iff {\log }_2\left(x^2\right)+{\log }_{2^{-1}}\left(2x+8\right)=0$

⇔ log₂ (x²) – log₂ (2x + 8) = 0

⇔ log₂ (x²) = log₂ (2x + 8)

$\iff \left\{\begin{array}{l}{x}^2=2x+8\\ 2x+8>0\end{array}\right.\iff \left\{\begin{array}{l}{x}^2-2x-8=0\\ x>-4\end{array}\right.$

$\iff \left\{\begin{array}{l}\left[\begin{array}{l}x=-2\\ x=4\end{array}\right.\\ x>-4\end{array}\right.\iff \left[\begin{array}{l}x=-2\\ x=4\end{array}\right.$

Vậy phương trình có nghiệm x ∈ {– 2; 4}.

Bài 63 trang 50 SBT Toán 11 Tập 2: Giải mỗi bất phương trình sau:

Lời giải:

a) (0,2)^{2x + 1} > 1 ⇔ (0,2)^{2x + 1} > 0,2⁰

⇔ 2x + 1 < 0 (do 0 < 0,2 < 1)

⇔ $x<-\frac{1}{2}$ .

Vậy bất phương trình có tập nghiệm $\left(-\infty ;-\frac{1}{2}\right)$ .

b) ${27}^{2x}\le \frac{1}{9}\iff {\left(3^3\right)}^{2x}\le 9^{-1}$

$\iff 3^{\mathrm{3..2}x}\le {\left(3^2\right)}^{-1}\iff 3^{6x}\le 3^{-2}$

$\iff 6x\le -2$(do 3 > 1)

$\iff x\le -\frac{1}{3}.$

Vậy bất phương trình có tập nghiệm $\left(-\infty ;-\frac{1}{3}\right]$ .

c) ${\left(\frac{1}{2}\right)}^{x^2-5x+4}\ge 4\iff {\left(2^{-1}\right)}^{x^2-5x+4}\ge 2^2$

$\iff 2^{-x^2+5x-4}\ge 2^2$

⇔ –x² + 5x – 4 ≥ 2 (vì 2 > 0)

⇔ –x² + 5x – 6 ≥ 0

⇔ 2 ≤ x ≤ 3.

Vậy bất phương trình có tập nghiệm [2; 3].

d) ${\left(\frac{1}{25}\right)}^{x+1}<{125}^{2x}\iff {\left(5^{-2}\right)}^{x+1}<{\left(5^3\right)}^{2x}$

⇔ 5^{–2x – 2} < 5^6x ⇔ –2x – 2 < 6x (do 5 > 1)

$\iff -8x<2\iff x>-\frac{1}{4}$

Vậy bất phương trình có tập nghiệm $\left(-\frac{1}{4};+\infty \right)$ .

e) ${\left(\sqrt{2}-1\right)}^{3x-2}<{\left(\sqrt{2}+1\right)}^{4-x}$

⇔ 2 – 3x < 4 – x

⇔ –2x < 2 ⇔ x > –1.

Vậy bất phương trình có tập nghiệm (–1; +∞).

⇔ x – 2x² > 2x – 6

⇔ – 2x² – x + 6 > 0

$\iff -2<x<\frac{3}{2}.$

Vậy bất phương trình có tập nghiệm $\left(-2;\frac{3}{2}\right).$

Bài 64 trang 51 SBT Toán 11 Tập 2: Giải mỗi bất phương trình sau:

a) ${\log }_{\frac{1}{2}}\left(2x-6\right)<-3;$

b) log₃ (x² – 2x + 2) > 0;

c) ${\log }_4\left(2x^2+3x\right)\ge \frac{1}{2};$

d) log_0,5 (x – 1) ≥ log_0,5 (5 – 2x);

e) log(x² + 1) ≤ log(x + 3);

g) ${\log }_{\frac{1}{5}}\left(x^2-6x+8\right)+{\log }_5\left(x-4\right)>0.$

Lời giải:

a) ${\log }_{\frac{1}{2}}\left(2x-6\right)<-3\iff 2x-6>{\left(\frac{1}{2}\right)}^{-3}$ (do $0<\frac{1}{2}<1)$

⇔ 2x – 6 > 8 ⇔ x > 7.

Vậy tập nghiệm của bất phương trình là (7; +∞).

b) log₃ (x² – 2x + 2) > 0

⇔ x² – 2x + 2 > 3⁰ ⇔ x² – 2x + 2 > 1

⇔ x² – 2x + 1 > 0 ⇔ (x – 1)² > 0 ⇔ x ≠ 1.

Vậy tập nghiệm của bất phương trình là ℝ \ {1}.

c) ${\log }_4\left(2x^2+3x\right)\ge \frac{1}{2}\iff 2x^2+3x\ge 4^{\frac{1}{2}}$

$\iff 2x^2+3x-2\ge 0\iff \left[\begin{array}{l}x\le -2\\ x\ge \frac{1}{2}\end{array}\right..$

Vậy tập nghiệm của bất phương trình là $\left(-\infty ;-2\right]\cup \left[\frac{1}{2};+\infty \right).$

d) log_0,5 (x – 1) ≥ log_0,5 (5 – 2x)

⇔ 0 < x – 1 ≤ 5 – 2x (Vì 0 < 0,5 < 1)

$\iff \left\{\begin{array}{l}x-1>0\\ x-1\le 5-2x\end{array}\right.\iff \left\{\begin{array}{l}x>1\\ 3x\le 6\end{array}\right.\iff \left\{\begin{array}{l}x>1\\ x\le 2\end{array}\right.\iff 1<x\le 2$

Vậy tập nghiệm của bất phương trình là (1 ; 2].

e) log(x² + 1) ≤ log(x + 3)

⇔ 0 < x² + 1 ≤ x + 3

⇔ x² – x – 2 ≤ 0 (do x² + 1 > 0 với mọi x)

⇔ –1 ≤ x ≤ 2.

Vậy tập nghiệm của bất phương trình là [–1; 2].

g) ${\log }_{\frac{1}{5}}\left(x^2-6x+8\right)+{\log }_5\left(x-4\right)>0$

$\iff {\log }_{5^{-1}}\left(x^2-6x+8\right)+{\log }_5\left(x-4\right)>0$

⇔ – log₅ (x² – 6x + 8) + log₅ (x – 4) > 0

⇔ log₅ (x² – 6x + 8) < log₅ (x – 4)

⇔ 0 < x² – 6x + 8 < x – 4

$\iff \left\{\begin{array}{l}{x}^2–6x+8>0\\ x^2–6x+8<x-4\end{array}\right.\iff \left\{\begin{array}{l}\left[\begin{array}{l}x>4\\ x<2\end{array}\right.\\ x^2-7x+12<0\end{array}\right.\iff \left\{\begin{array}{l}\left[\begin{array}{l}x>4\\ x<2\end{array}\right.\\ 3<x<4\end{array}\right.\iff x\in \varnothing .$

Vậy bất phương trình vô nghiệm.

Bài 65 trang 51 SBT Toán 11 Tập 2: Người ta nuôi cấy vi khuẩn Bacillus subtilis trong nồi lên men và thu được số liệu sau: Lúc ban đầu, số tế bào/1 ml dịch nuôi là 2.10². Sau 13 giờ, số tế bào/1 ml dịch nuôi là 3,33.10⁹. Biết vi khuẩn Bacillus subtilis sinh trưởng trong điều kiện tối ưu và sinh sản theo hình thức tự nhân đôi. Hỏi sau bao nhiêu phút, vi khuẩn Bacillus subtilis tự nhân đôi một lần (làm tròn kết quả đến hàng đơn vị)?

Lời giải:

Đổi 13 giờ = 780 phút.

Gọi T (phút) là thời gian để vi khuẩn Bacillus subtilis tự nhân đôi một lần.

Gọi M₀ là số tế bào/1 ml dịch nuôi của vi khuẩn Bacillus subtilis tại thời điểm ban đầu (t = 0). Theo bài ra ta có: M₀ = 2.10².

Gọi M_t là số tế bào/1 ml dịch nuôi của vi khuẩn Bacillus subtilis tại thời điểm t.

Sau 13 giờ, số tế bào/1 ml dịch nuôi là 3,33.10⁹ nên ta có: M₇₈₀ = 3,33 . 10⁹.

Do vi khuẩn Bacillus subtilis sinh trưởng trong điều kiện tối ưu và sinh sản theo hình thức tự nhân đôi nên ta có: $M_t=M_0{.2}^{\frac{t}{T}}.$

Suy ra: $M_{780}=M_0{.2}^{\frac{780}{T}}\Rightarrow 3,{33.10}^9={2.10}^2{.2}^{\frac{780}{T}}$

$\Rightarrow 2^{\frac{780}{T}}=1,{665.10}^7.$

$\Rightarrow \frac{780}{T}={\log }_2(1,{665.10}^7)\Rightarrow T\approx 33.$

Vậy sau gần 33 phút vi khuẩn Bacillus subtilis tự nhân đôi một lần.

Bài 66 trang 51 SBT Toán 11 Tập 2: Tốc độ của gió S (dặm/giờ) gần tâm của một con lốc xoáy được tính bởi công thức S = 93logd + 65, trong đó d (dặm) là quãng đường cơn lốc xoáy đó di chuyển được.

(Nguồn: Ron Larson, Intermediate Algebra, Cengate)

Tính quãng đường cơn lốc xoáy đã di chuyển được, biết tốc độ của gió ở gần tâm bằng 140 dặm/giờ (làm tròn kết quả đến hàng phần mười).

Lời giải:

Ta có: S = 93logd + 65, trong đó d (dặm) là quãng đường cơn lốc xoáy đó di chuyển được.

Với S = 140 (dặm/giờ) suy ra: 93logd + 65 = 140

$\Rightarrow \log d=\frac{75}{93}\Rightarrow d={10}^{\frac{75}{93}}\approx 6,4$ (dặm).

Vậy khi tốc độ của gió ở gần tâm bằng 140 dặm/giờ thì cơn lốc xoáy di chuyển được quãng đường gần bằng 6,4 dặm.

Bài 67 trang 51 SBT Toán 11 Tập 2: Dân số thành phố Hà Nội năm 2022 khoảng 8,4 triệu người. Giả sử tỉ lệ tăng dân số hằng năm của Hà Nội không đổi và bằng r = 1,04%. Biết rằng, sau t năm dân số Hà Nội (tính từ mốc năm 2022) ước tính theo công thức: S = A . e^rt, trong đó A là dân số năm lấy làm mốc. Hỏi từ năm nào trở đi, dân số Hà Nội vượt quá 10 triệu người?

Lời giải:

Vì sau t năm dân số Hà Nội (tính từ mốc năm 2022) ước tính theo công thức:

S = A . e^rt, trong đó A là dân số năm lấy làm mốc.

Suy ra: A = 8,4 (triệu người).

Theo bài ra ta có: $8,4\cdot e^{\frac{1,04}{100}.t}>10$

$\Rightarrow e^{\frac{1,04}{100}.t}>\frac{25}{21}\Rightarrow \frac{1,04}{100}.t>\ln \frac{25}{21}$

$\Rightarrow t>\frac{1250}{13}\cdot \ln \frac{25}{21}$

Suy ra t > 16,765.

Vậy sau khoảng 17 năm tính từ mốc năm 2022, tức là từ năm 2039 thì dân số Hà Nội vượt quá 10 triệu người.

Bài 68 trang 51 SBT Toán 11 Tập 2: Mức cường độ âm L (dB) được tính bởi công thức $L=10\log \frac{I}{{10}^{-12}},$ trong đó I (W/m²) là cường độ âm. Để đảm bảo sức khỏe cho công nhân, mức cường độ âm trong một nhà máy phải giữ sao cho không vượt quá 85 dB. Hỏi cường độ âm của nhà máy đó phải thỏa mãn điều kiện nào để đảm bảo sức khỏe cho công nhân?

Lời giải:

Vì mức cường độ âm trong một nhà máy phải giữ sao cho không vượt quá 85 dB nên ta có: $L\le 85\iff 10\log \frac{I}{{10}^{-12}}\le 85$

$\iff \log \frac{I}{{10}^{-12}}\le 8,5\iff \log I-\log {10}^{-12}<8,5$

$\iff \log I+12\le 8,5\iff \log I\le -3,5\iff I\le {10}^{-3,5}$

Vậy cường độ âm của nhà máy đó không vượt quá 10^–3,5 (W/m²).

Xem thêm các bài giải SBT Toán lớp 11 Cánh diều hay, chi tiết khác: