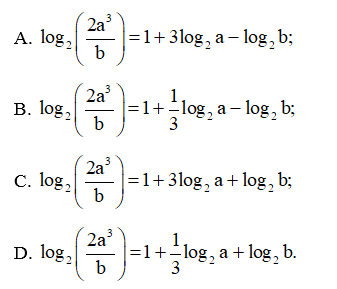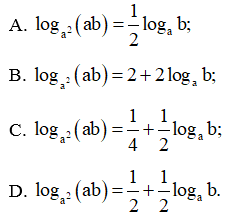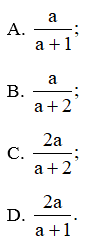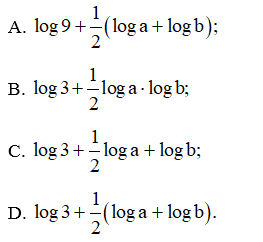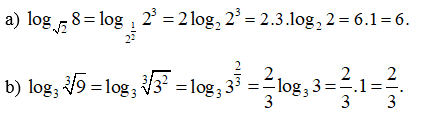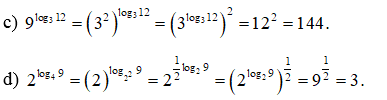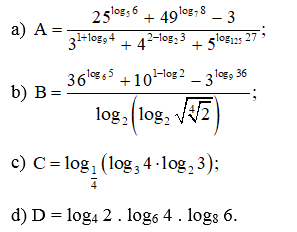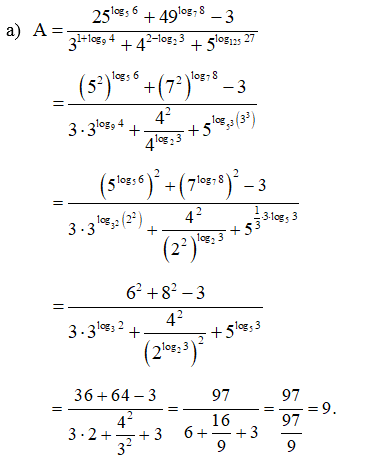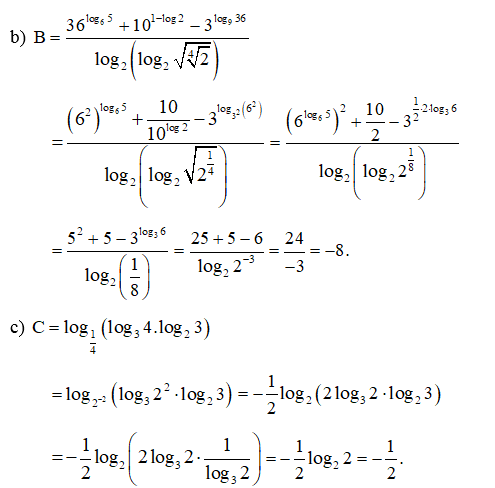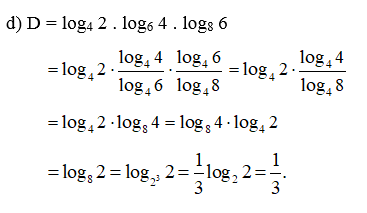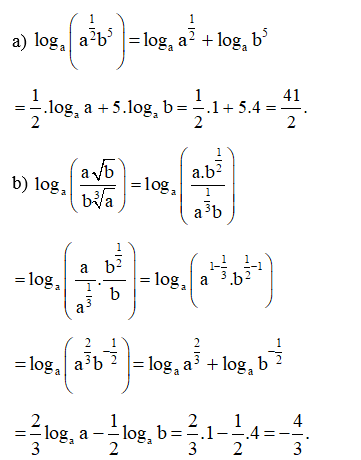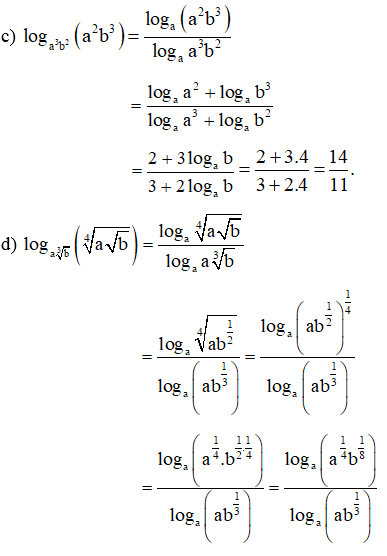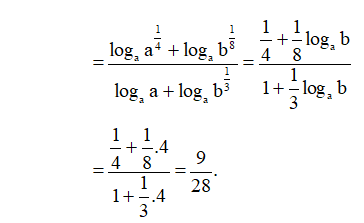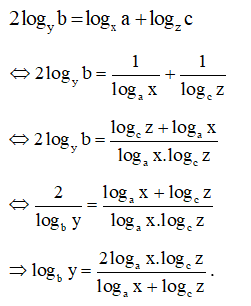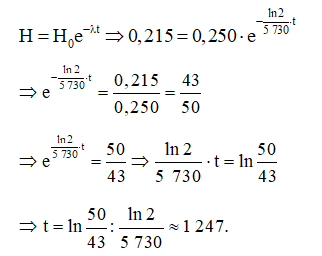Giải SBT Toán 11 (Cánh diều) Bài 2: Phép tính lôgarit

Giải SBT Toán 11 Bài 2: Phép tính lôgarit

Bài 17 trang 37 SBT Toán 11 Tập 2: Cho a > 0, a ≠ 2. Giá trị của ${\log }_{\frac{a}{2}}\left(\frac{a^2}{4}\right)$ bằng:

A. $\frac{1}{2}$

B. 2;

C. $-\frac{1}{2};$

D. – 2.

Lời giải:

Đáp án đúng là: B

Với a > 0, a ≠ 2 ta có: ${\log }_{\frac{a}{2}}\left(\frac{a^2}{4}\right)={\log }_{\frac{a}{2}}\left(\frac{a^2}{2^2}\right)={\log }_{\frac{a}{2}}{\left(\frac{a}{2}\right)}^2=2.$

Bài 18 trang 37 SBT Toán 11 Tập 2: Cho a > 0, a ≠ 1. Giá trị của ${\log }_a\sqrt{a\sqrt{a}}$ bằng:

A. $\frac{4}{3}$

B. $\frac{3}{2}$

C. $\frac{3}{4}$

D. $\frac{1}{8}$

Lời giải:

Đáp án đúng là: C

Với a > 0, a ≠ 1 ta có:

${\log }_a\sqrt{a\sqrt{a}}={\log }_a{\left(a.a^{\frac{1}{2}}\right)}^{\frac{1}{2}}={\log }_a{\left(a^{\frac{3}{2}}\right)}^{\frac{1}{2}}$$={\log }_a{a}^{\frac{3}{2}.\frac{1}{2}}=lo{g}_a{a}^{\frac{3}{4}}=\frac{3}{4}.$

Bài 19 trang 37 SBT Toán 11 Tập 2: Cho a > 0. Giá trị của ${\log }_2\left(\frac{8}{a}\right)$ bằng:

A. 3 – log₂ a;

B. 4 – log₂ a;

C. $\frac{1}{{\log }_{2}a};$

D. 8 – log₂ a.

Lời giải:

Đáp án đúng là: A

Với a > 0 ta có:

${\log }_2\left(\frac{8}{a}\right)={\log }_{2}8-{\log }_{2}a={\log }_2{2}^3-{\log }_{2}a$

= 3log₂2 – log₂ a = 3 – log₂ a.

Bài 20 trang 37 SBT Toán 11 Tập 2: Nếu log_ab = 2, log_ac = 3, thì log_a(b²c³) bằng:

A. 108;

B. 13;

C. 31;

D. 36.

Lời giải:

Đáp án đúng là: B

Với a > 0, b > 0, c > 0, a ≠ 1 ta có:

log_a(b²c³) = log_ab² + log_ac³ = 2log_ab + 3log_ac = 2.2 + 3.3 = 13.

Bài 21 trang 38 SBT Toán 11 Tập 2: Cho a > 0. Giá trị của ln(9a) – ln(3a) bằng:

A. ln(6a);

B. ln6;

C. $\frac{\ln 9}{\ln 3};$

D. ln3.

Lời giải:

Đáp án đúng là: D

Với a > 0 ta có:

ln(9a) – ln(3a) = ln(3.3a) – ln(3a)

= ln3 + ln(3a) – ln(3a) = ln3.

Bài 22 trang 38 SBT Toán 11 Tập 2: Cho a > 0, b > 0. Mệnh đề đúng là:

Lời giải:

Đáp án đúng là: A

Với a > 0, b > 0 ta có:

${\log }_2\left(\frac{2a^3}{b}\right)={\log }_2\left(2a^3\right)-{\log }_{2}b$

= log₂2 + log₂a³ – log₂b = 1 + 3log₂a – log₂b.

Bài 23 trang 38 SBT Toán 11 Tập 2: Cho a > 0, a ≠ 1 và b > 0. Mệnh đề đúng là:

Lời giải:

Đáp án đúng là: D

Với a > 0, a ≠ 1 và b > 0 ta có:

${\log }_{a^2}\left(ab\right)=\frac{1}{2}{\log }_a\left(ab\right)=\frac{1}{2}\left({\log }_{a}a+{\log }_{a}b\right)$

$=\frac{1}{2}\left(1+lo{g}_{a}b\right)=\frac{1}{2}+\frac{1}{2}{\log }_{a}b.$

Bài 24 trang 38 SBT Toán 11 Tập 2: Nếu log₂3 = a thì log₆9 bằng:

Lời giải:

Đáp án đúng là: D

Nếu log₂3 = a thì ${\log }_{6}9=\frac{{\log }_{2}9}{{\log }_{2}6}=\frac{{\log }_2{3}^2}{{\log }_{2}3+lo{g}_{2}2}$

$=\frac{2{\log }_{2}3}{{\log }_{2}3+1}=\frac{2a}{a+1}.$

Bài 25 trang 38 SBT Toán 11 Tập 2: Nếu log_ab = 5 thì ${\log }_{a^{2}b}\left(a{b}^2\right)$ bằng:

A. $\frac{11}{7}$

B. 1;

C. 4;

D. $\frac{26}{7}$

Lời giải:

Đáp án đúng là: A

Với a > 0, b > 0, a ≠ 1 và log_ab = 5 thì

${\log }_{a^{2}b}\left(a{b}^2\right)=\frac{{\log }_a\left(a{b}^2\right)}{{\log }_a\left(a^{2}b\right)}=\frac{{\log }_{a}a+{\log }_a{b}^2}{{\log }_a{a}^2+{\log }_{a}b}$

$=\frac{1+2{\log }_{a}b}{2+lo{g}_{a}b}=\frac{1+2\cdot 5}{2+5}=\frac{11}{7}.$

Bài 26 trang 38 SBT Toán 11 Tập 2: Cho a > 0, b > 0 thỏa mãn a² + b² = 7ab. Khi đó, log(a+b) bằng:

Lời giải:

Đáp án đúng là: D

Với a > 0, b > 0 ta có:

a² + b² = 7ab hay a² + 2ab + b² = 9ab ⇒ (a + b)² = 9ab.

$\Rightarrow a+b=\sqrt{9ab}\Rightarrow a+b=3{\left(ab\right)}^{\frac{1}{2}}$ (Vì a > 0, b > 0).

Xét: $\log \left(a+b\right)=\log \left[3{\left(ab\right)}^{\frac{1}{2}}\right]$

$=\log 3+\log {\left(ab\right)}^{\frac{1}{2}}$

$=\log 3+\frac{1}{2}\left(\log a+\log b\right).$

Bài 27 trang 38 SBT Toán 11 Tập 2: Không sử dụng máy tính cầm tay, hãy tính:

Lời giải:

Bài 28 trang 38 SBT Toán 11 Tập 2: Tính:

Lời giải:

Bài 29 trang 39 SBT Toán 11 Tập 2: Cho log_ab = 4. Tính:

Lời giải:

Bài 30 trang 39 SBT Toán 11 Tập 2: a) Cho log₂3 = a. Tính log₁₈72 theo a

b*) Cho log2 = a. Tính log₂₀50 theo a.

Lời giải:

a) ${\log }_{18}72=\frac{{\log }_{2}72}{{\log }_{2}18}=\frac{{\log }_2\left(2^3{.3}^2\right)}{{\log }_2\left({2.3}^2\right)}$

$=\frac{{\log }_2{2}^3+{\log }_2{3}^2}{{\log }_{2}2+{\log }_2{3}^2}=\frac{3+2{\log }_{2}3}{1+2{\log }_{2}3}=\frac{3+2a}{1+2a}.$

b*) Ta có: 1 = log10 = log(2.5) = log2 + log5 nên log5 = 1 – log2 = 1 – a.

Xét: ${\log }_{20}50=\frac{\log 50}{\log 20}=\frac{\log \left(10.5\right)}{\log \left(10.2\right)}$

$=\frac{\log 10+\log 5}{\log 10+\log 2}=\frac{1+1-a}{1+a}=\frac{2-a}{1+a}.$

Bài 31 trang 39 SBT Toán 11 Tập 2: Cho x > 0, y > 0 thoả mãn: x² + 4y² = 6xy. Chứng minh rằng:

2log(x + 2y) = 1 + logx + logy.

Lời giải:

Với x > 0, y > 0 ta có:

x² + 4y² = 6xy ⇒ x² + 4xy + 4y² = 10xy

⇒ (x + 2y)² = 10xy.

Suy ra: 2log(x + 2y) = log(x + 2y)²

= log(10xy) = log10 + logx + logy

= 1 + logx + logy.

Vậy 2log(x + 2y) = 1 + logx + logy.

Bài 32 trang 39 SBT Toán 11 Tập 2: Cho a, b, c, x, y, z là các số thực dương khác 1 và log_xa, log_yb, log_zc theo thứ tự lập thành một cấp số cộng. Chứng minh rằng:

${\log }_{b}y=\frac{2{\log }_{a}x\cdot {\log }_{c}z}{{\log }_{a}x+{\log }_{c}z}.$

Lời giải:

Do log_xa, log_yb, log_zc theo thứ tự lập thành một cấp số cộng nên ta có:

Bài 33 trang 39 SBT Toán 11 Tập 2: Để tính độ tuổi của mẫu vật bằng gỗ, người ta đo độ phóng xạ ${}_6{}^{14}C$ có trong mẫu vật tại thời điểm t (năm) (so với thời điểm ban đầu t = 0), sau đó sử dụng công thức tính độ phóng xạ $H=H_0{e}^{-\lambda t}$ (đơn vị là Becquerel, kí hiệu Bq) với H₀ là độ phóng xa ban đầu (tại thời điểm t = 0); $\lambda =\frac{\ln 2}{T}$ là hằng số phóng xạ, T = 5 730 (năm) (Nguồn: Vật lí 12 Nâng cao, NXBGD Việt Nam, 2014). Khảo sát một mẫu gỗ cổ, các nhà khoa học đo được độ phóng xạ là 0,215 Bq. Biết độ phóng xạ của mẫu gỗ tươi cùng loại là 0,250 Bq. Xác định độ tuổi của mẫu gỗ cổ đó (làm tròn kết quả đến hàng đơn vị).

Lời giải:

Chất phóng xạ có chu kì bán rã là T = 5 730 (năm).

Suy ra: $\lambda =\frac{\ln 2}{5730}.$

Gọi t là độ tuổi của mẫu gỗ cổ.

Vì độ phóng xạ của mẫu gỗ tươi cùng loại là 0,250 Bq nên ta có H₀ = 0,250 Bq.

Khi khảo sát một mẫu gỗ cổ, các nhà khoa học đo được độ phóng xa là 0,215 Bq, suy ra ta có H = 0,215 Bq.

Ta có:

Vậy độ tuổi của mẫu gỗ cổ đó xấp xỉ 1 247 năm.

Xem thêm các bài giải SBT Toán lớp 11 Cánh diều hay, chi tiết khác: