Giải SBT Toán 10 (Cánh diều) Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng

Giải Sách bài tập Toán 10 Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng

Giải SBT Toán 10 trang 81 Tập 2

Bài 33 trang 81 SBT Toán 10 Tập 2: Phương trình nào dưới đây là phương trình tham số của một đường thẳng song song với đường thẳng x – 2y + 3 = 0?

A. $\left\{\begin{array}{c}x=-1+2t\\ y=1+t\end{array}\right.$ ;

B. $\left\{\begin{array}{c}x=1+2t\\ y=-1+t\end{array}\right.$ ;

C. $\left\{\begin{array}{c}x=1+t\\ y=-1-2t\end{array}\right.$ ;

D. $\left\{\begin{array}{c}x=1-2t\\ y=-1+t\end{array}\right.$ .

Lời giải:

Gọi d là đường thẳng cần tìm song song với đường thẳng x – 2y + 3 = 0

Do đó d có vectơ pháp tuyến là: $\overrightarrow{n}=\left(1;-2\right)$ .

Do đó d có vectơ chỉ phương là $\overrightarrow{u}=k\left(2;1\right)$ .

Như vậy chỉ có phương án A và B là thỏa mãn có vectơ chỉ phương là $\overrightarrow{u}=k\left(2;1\right)$ . Do đó đáp án C và D sai.

Xét $\left\{\begin{array}{c}x=-1+2t\\ y=1+t\end{array}\right.$  đi qua điểm (-1; 1). Mà điểm (-1; 1) thuộc đường thẳng x – 2y + 3 = 0 vì -1 – 2.1 + 3 = 0 = 0 (luôn đúng).

Do đó đường thẳng ở câu A trùng với đường thẳng x – 2y + 3 = 0.

Xét $\left\{\begin{array}{c}x=1+2t\\ y=-1+t\end{array}\right.$ đi qua điểm (1; -1).

Thay x = 1 và y = - 1 vào phương trình đường thẳng x – 2y + 3 = 0, ta được: 1 – 2.(-1) + 3 = 0 ( vô lí). Do đó đường thẳng ý b song song với đường thẳng x – 2y + 3 = 0.

Vậy chọn đáp án B.

Bài 34 trang 81 SBT Toán 10 Tập 2: Phương trình nào dưới đây là phương trình tham số của một đường thẳng vuông góc với đường thẳng $\left\{\begin{array}{c}x=-1+3t\\ y=1-2t\end{array}\right.$  ?

A. $\left\{\begin{array}{c}x=-1-2t\\ y=1-3t\end{array}\right.$ ;

B. $\left\{\begin{array}{c}x=-1-2t\\ y=1+3t\end{array}\right.$ ;

C. $\left\{\begin{array}{c}x=-1-3t\\ y=1+2t\end{array}\right.$ ;

D. $\left\{\begin{array}{c}x=-1-3t\\ y=1-2t\end{array}\right.$ .

Lời giải:

Xét phương trình đường thẳng $\left\{\begin{array}{c}x=-1+3t\\ y=1-2t\end{array}\right.$  có vectơ chỉ phương $\overrightarrow{u}$ = (3; - 2).

Gọi d là đường thẳng cần tìm vuông góc với đường thẳng đã cho.

Do đó d có vectơ chỉ phương vuông góc với vectơ chỉ phương của đường thẳng đã cho nên vectơ chỉ phương của d là: $\overrightarrow{u_1}=k\left(2;3\right)$  với k ∈ ℝ.

Xét các đáp án chỉ có đáp án A thỏa mãn có vectơ chỉ phương $\overrightarrow{u}=\left(-2;-3\right)$ là đúng với k = -1.

Vậy chọn đáp án A.

Bài 35 trang 81 SBT Toán 10 Tập 2: Đường thẳng ∆ đi qua điểm M(- 1; 2) và song song với đường thẳng d: 2x – y – 5 = 0 có phương trình tổng quát là:

A. 2x – y = 0;

B. 2x – y + 4 = 0;

C. 2x + y + 4 = 0;

D. x + 2y – 3 = 0.

Lời giải:

Xét đường thẳng d: 2x – y – 5 = 0 có vectơ pháp tuyến $\overrightarrow{n_d}=\left(2;-1\right)$ .

Vì ∆ // d nên vectơ pháp tuyến của ∆ là $\overrightarrow{n}=\left(2;-1\right)$ .

Đường thẳng ∆ đi qua M( -1; 2) và nhận $\overrightarrow{n}=\left(2;-1\right)$  làm vectơ pháp tuyến nên có phương trình tổng quát là: 2(x + 1) – (y – 2) = 0 hay 2x – y + 4 = 0.

Vậy chọn đáp án B.

Bài 36 trang 81 SBT Toán 10 Tập 2: Đường thẳng ∆ đi qua điểm M(3; - 4) và vuông góc với đường thẳng d: x – 3y + 1 = 0 có phương trình tổng quát là:c

A. x – 3y – 15 = 0;

B. – 3x + y + 5 = 0;

C. 3x + y – 13 = 0;

D. 3x + y – 5 = 0.

Lời giải:

Đường thẳng ∆ vuông góc với đường thẳng d: x – 3y + 1 = 0

Nên đường thẳng ∆ có vectơ pháp tuyến là: $\overrightarrow{n}=\left(3;1\right)$ .

Đường thẳng ∆ đi qua M( 3; - 4) nên có phương trình tổng quát là:

3(x - 3) + (y + 4) = 0 hay 3x + y - 5 = 0.

Vậy chọn đáp án D.

Bài 37 trang 81 SBT Toán 10 Tập 2: Cho ∆₁: x – 2y + 3 = 0 và ∆₂: – 2x – y + 5 = 0. Số đo góc giữa hai đường thẳng ∆₁ và ∆₂ là:

A. 30⁰;

B. 45⁰;

C. 90⁰;

D. 60⁰.

Lời giải:

Ta thấy vectơ pháp tuyến của ${\Delta }_1$  là:  $\overrightarrow{n_1}=\left(1;-2\right)$

Vectơ pháp tuyến của ${\Delta }_1$  là: $\overrightarrow{n_2}=\left(-2;-1\right)$

Ta có:  $\overrightarrow{n_1}.\overrightarrow{n_2}=1.\left(-2\right)+\left(-2\right).\left(-1\right)=0$

Suy ra $\overrightarrow{n_1}$  vuông góc với  $\overrightarrow{n_2}$

Vậy 2 đường thẳng trên vuông góc với nhau, chọn đáp án C.

Giải SBT Toán 10 trang 82 Tập 2

Bài 38 trang 82 SBT Toán 10 Tập 2: Cho ${\Delta }_1:\left\{\begin{array}{c}x=-2+\sqrt{3}t\\ y=1-t\end{array}\right.$  và ${\Delta }_2:\left\{\begin{array}{c}x=-1+\sqrt{3}t\text{'}\\ y=2+t\text{'}\end{array}\right.$ . Số đo góc giữa hai đường thẳng ∆₁ và ∆₂ là:

A. 30⁰;

B. 45⁰;

C. 90⁰;

D. 60⁰.

Lời giải:

Ta thấy vectơ chỉ phương của ${\Delta }_1$  là:  $\overrightarrow{u_1}=\left(\sqrt{3};-1\right)$

Vectơ chỉ phương của ${\Delta }_2$  là: $\overrightarrow{u_2}=\left(\sqrt{3};1\right)$

Ta có: cos $\left(\overrightarrow{u_1},\overrightarrow{u_2}\right)=\frac{\overrightarrow{u_1}.\overrightarrow{u_2}}{\left|\overrightarrow{u_1}\right|.\left|\overrightarrow{u_2}\right|}=\frac{\sqrt{3}.\sqrt{3}+\left(-1\right).1}{\sqrt{3+1}.\sqrt{3+1}}=\frac{2}{4}=\frac{1}{2}$   

Suy ra góc giữa 2 đường thẳng chính là góc nhọn giữa 2 vectơ chỉ phương của 2 đường thẳng đó.

Do đó $\left({\Delta }_1,{\Delta }_2\right)=\left(\overrightarrow{u_1},\overrightarrow{u_2}\right)={60}^o$

Vậy chọn đáp án D.

Bài 39 trang 82 SBT Toán 10 Tập 2: Khoảng cách từ điểm M(5; - 2) đến đường thẳng ∆: - 3x + 2y + 6 = 0 là:

A. 13;

B. $\sqrt{13}$ ;

C. $\frac{\sqrt{13}}{13}$ ;

D. $2\sqrt{13}$ .

Lời giải:

Áp dụng công thức ta có:

d(M, ∆)=  $\frac{\left|\left(-3\right).5+2.\left(-2\right)+6\right|}{\sqrt{{\left(-3\right)}^2+2^2}}=\frac{13}{\sqrt{13}}=\sqrt{13}$

Vậy chọn đáp án B.

Bài 40 trang 82 SBT Toán 10 Tập 2: Xét vị trí tương đối của mỗi cặp đường thẳng sau:

a) d₁: 2x – 3y + 5 = 0 và d₂: 2x + y – 1 = 0;

b) $d_3:\left\{\begin{array}{c}x=-1-3t\\ y=3+t\end{array}\right.$  và d₄: x + 3y – 5 = 0;

c) $d_5:\left\{\begin{array}{c}x=2-2t\\ y=-1+t\end{array}\right.$  và  $d_6:\left\{\begin{array}{c}x=-2+2t\text{'}\\ y=1-t\text{'}\end{array}\right.$.

Lời giải:

a) Vectơ pháp tuyến của $d_1$  là: $\overrightarrow{n_1}=\left(2;-3\right)$  

Vectơ pháp tuyến của $d_2$  là: $\overrightarrow{n_2}=\left(2;1\right)$

Ta có: $\frac{2}{2}\ne \frac{-3}{1}$  suy ra hai vectơ $\overrightarrow{n_1}$  và $\overrightarrow{n_2}$  không cùng phương.

Do đó $d_1$  và $d_2$  cắt nhau.

b) Vectơ chỉ phương của $d_3$  là: $\overrightarrow{u_3}=\left(-3;1\right)$  nên vectơ pháp tuyến của $d_3$  là: $\overrightarrow{n_3}=\left(1;3\right)$ .

Vectơ pháp tuyến của $d_4$  là: $\overrightarrow{n_4}=\left(1;3\right)$

Ta có $\overrightarrow{n_3}=\overrightarrow{n_4}$ nên $\overrightarrow{n_3}$  và $\overrightarrow{n_4}$  cùng phương hay d₃ song song hoặc trùng d­₄.

Lấy điểm A(-1; 3) thuộc $d_4$ .

Thay tọa độ A(-1; 3) vào  ta có: - 1 + 3.3 – 5 = 3 = 0 (vô lí).

Suy ra A(-1; 3) không thuộc $d_4$ .

Vậy 2 đường thẳng trên song song.

c) Vectơ chỉ phương của $d_5$  là  $\overrightarrow{u_5}=\left(-2;1\right)$

Vectơ chỉ phương của $d_6$  là $\overrightarrow{u_6}=\left(2;-1\right)$

Ta thấy $\overrightarrow{u_5}=\left(-1\right).\overrightarrow{u_6}$  nên 2 vectơ $\overrightarrow{u_5}$  và  $\overrightarrow{u_6}$ cùng phương. Do đó hai đường thẳng d₅ và d₆ song song hoặc trùng nhau.

Lấy điểm M(2; -1) thuộc đường thẳng d₅. Thay tọa độ điểm M vào phương trình tham số của $d_6$  ta có:

$\left\{\begin{array}{l}2=-2+2t\text{'}\\ -1=1-t\text{'}\end{array}\right.\iff \left\{\begin{array}{l}t\text{'}=2\\ t\text{'}=2\end{array}\right.\iff t\text{'}=2$

Suy ra M thuộc $d_6$ .

Vậy d₅ trùng d₆.

Bài 41 trang 82 SBT Toán 10 Tập 2: Tìm số đo góc giữa hai đường thẳng của mỗi cặp đường thẳng sau:

a) ∆₁: 3x + y – 5 = 0 và ∆₂: x + 2y – 3 = 0;

b) ${\Delta }_3:\left\{\begin{array}{c}x=2+\sqrt{3}t\\ y=-1+3t\end{array}\right.$  và ${\Delta }_4:\left\{\begin{array}{c}x=3-\sqrt{3}t\text{'}\\ y=-t\text{'}\end{array}\right.$ ;

c) ${\Delta }_5:-\sqrt{3}x+3y+2=0$  và ${\Delta }_6:\left\{\begin{array}{c}x=3t\\ y=1-\sqrt{3}t\end{array}\right.$ .

Lời giải:

a) Vectơ pháp tuyến của ${\Delta }_1$  là  $\overrightarrow{n_1}=\left(3;1\right)$

Vectơ pháp tuyến của ${\Delta }_2$  là $\overrightarrow{n_2}=\left(1;2\right)$

Góc giữa 2 đường thẳng là:

 $\cos \left({\Delta }_1,{\Delta }_2\right)=\left|\cos \left(\overrightarrow{n_1},\overrightarrow{n_2}\right)\right|=\frac{\left|3.1+1.2\right|}{\sqrt{3^2+1^2}.\sqrt{1^2+2^2}}=\frac{5}{\sqrt{10}.\sqrt{5}}=\frac{1}{\sqrt{2}}$

Suy ra $\left({\Delta }_1,{\Delta }_2\right)={45}^o$ .

b) Vectơ chỉ phương của ${\Delta }_3$  là  $\overrightarrow{u_3}=\left(\sqrt{3};3\right)$

Vectơ chỉ phương của ${\Delta }_4$  là $\overrightarrow{u_4}=\left(-\sqrt{3};-1\right)$

Góc giữa 2 đường thẳng là:

 $\cos \left({\Delta }_1,{\Delta }_2\right)=\left|\cos \left(\overrightarrow{u_3},\overrightarrow{u_4}\right)\right|=\frac{\left|\sqrt{3}.\left(-\sqrt{3}\right)+3.\left(-1\right)\right|}{\sqrt{{\left(\sqrt{3}\right)}^2+3^2}.\sqrt{{\left(-\sqrt{3}\right)}^2+{\left(-1\right)}^2}}=\frac{\sqrt{3}}{2}$

Suy ra $\left({\Delta }_3,{\Delta }_4\right)={30}^o$ .

c) Vectơ pháp tuyến của ${\Delta }_5$  là  $\overrightarrow{n_5}=\left(-\sqrt{3};3\right)$

Vectơ chỉ phương của ${\Delta }_6$  là $\overrightarrow{u_6}=\left(3;-\sqrt{3}\right)$  nên vectơ pháp tuyến của ${\Delta }_6$  là $\overrightarrow{n_6}=\left(\sqrt{3};3\right)$ .

Góc giữa 2 đường thẳng là:

 $\cos \left({\Delta }_1,{\Delta }_2\right)=\left|\cos \left(\overrightarrow{n_5},\overrightarrow{n_6}\right)\right|=\frac{\left|\left(-\sqrt{3}\right).\sqrt{3}+3.3\right|}{\sqrt{{\left(-\sqrt{3}\right)}^2+3^2}.\sqrt{{\left(\sqrt{3}\right)}^2+3^2}}=\frac{6}{12}=\frac{1}{2}$

Suy ra $\left({\Delta }_1,{\Delta }_2\right)={60}^o$ .

Bài 42 trang 82 SBT Toán 10 Tập 2: Tính khoảng cách từ một điểm đến một đường thẳng trong các trường hợp sau:

a) A(- 3; 1) và ∆₁: 2x + y – 4 = 0;

b) B(1; - 3) và ${\Delta }_2:\left\{\begin{array}{c}x=-3+3t\\ y=1-t\end{array}\right.$ .

Lời giải:

a) Ta có: vectơ pháp tuyến của đường thẳng ${\Delta }_1$  là  $\overrightarrow{n_1}=\left(2;1\right)$

Suy ra $d\left(A,{\Delta }_1\right)=\frac{\left|2.\left(-3\right)+1-4\right|}{\sqrt{2^2+1^2}}=\frac{9}{\sqrt{5}}$ .

b) ${\Delta }_2$ có vectơ chỉ phương là $\overrightarrow{u_2}=\left(3;-1\right)$  và đi qua điểm A(-3; 1).

Vectơ pháp tuyến của đường thẳng là: $\overrightarrow{n_2}=\left(1;3\right)$ .

Suy ra phương trình đường thẳng ${\Delta }_2$  là: x + 3 + 3( y – 1) = 0 hay x + 3y = 0

$d\left(B,{\Delta }_2\right)=\frac{\left|1+3.\left(-3\right)\right|}{\sqrt{1^2+3^2}}=\frac{8}{\sqrt{10}}$.

Bài 43 trang 82 SBT Toán 10 Tập 2: Cho hai đường thẳng song song ∆₁: ax + by + c = 0 và ∆₂: ax + by + d = 0. Chứng minh rằng khoảng cách giữa hai đường thẳng ∆₁ và ∆₂ bằng $\frac{\left|d-c\right|}{\sqrt{a^2+b^2}}$ .

Lời giải:

Gọi M $\left(x_0;y_0\right)$ thuộc ∆₁  nên $a{x}_0+b{y}_0+c=0$ .

Khoảng cách giữa ∆₁  đến ∆₂  bằng khoảng cách từ M đến ∆₂  bằng

$d\left(M,{\Delta }_2\right)=\frac{\left|a{x}_0+b{y}_0+d\right|}{\sqrt{a^2+b^2}}=\frac{\left|a{x}_0+b{y}_0+c+d-c\right|}{\sqrt{a^2+b^2}}=\frac{\left|d-c\right|}{\sqrt{a^2+b^2}}$.

Vậy bài toán được chứng minh.

Bài 44 trang 82 SBT Toán 10 Tập 2: Cho hai đường thẳng ∆₁: mx – 2y – 1 = 0 và ∆₂: x – 2y + 3 = 0. Với giá trị nào của tham số m thì:

a) ∆₁ // ∆₂;

b) ∆₁ ⊥ ∆₂.

Lời giải:

Vectơ pháp tuyến của ∆₁  là: $\overrightarrow{n_1}=\left(m;-2\right)$ ;

Vectơ pháp tuyến của ∆₂  là: $\overrightarrow{n_2}=\left(1;-2\right)$ .

a) ∆₁ // ∆₂ khi $\overrightarrow{n_1}$  cùng phương với  $\overrightarrow{n_2}$

hay  $\frac{m}{1}=\frac{-2}{-2}\iff m=1$ .

Thay m = 1 vào lần lượt hai đường thẳng ∆₁ ta được: x – 2y – 1 = 0.

Lấy M(– 1; 1) thuộc ∆₂, thay x = – 1 và y = 1 vào ∆₁, ta được: – 1 – 2.1 – 1 = 0 (vô lí). Do đó M không thuộc ∆₁.

Vậy m = 1 thỏa mãn để ∆₁ // ∆₂.

b) ∆₁ vuông góc ∆₂ khi $\overrightarrow{n_1}$  vuông góc với $\overrightarrow{n_2}$  hay $\overrightarrow{n_1}.\overrightarrow{n_2}=0$

⇔ m.1 + (-2).(-2) = 0 ⇔  m = - 4.

Vậy với m= – 4 thì ∆₁ vuông góc ∆₂.

Bài 45 trang 82 SBT Toán 10 Tập 2: Cho ba điểm A(- 2; 2), B(4; 2), C(6; 4). Viết phương trình đường thẳng ∆ đi qua B đồng thời cách đều A và C?

Lời giải:

 cách đều A và C khi và chỉ khi đi qua trung điểm của AC hoặc song song với AC.

TH1: ∆ là đi qua trung điểm của AC

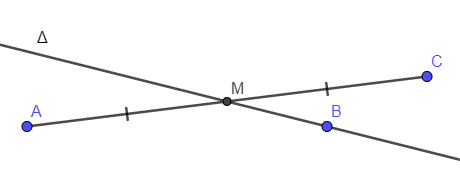
Gọi M là trung điểm của đoạn thẳng AB nên tọa độ điểm M là M(2; 3).

Vectơ chỉ phương của đường thẳng ∆ là:  $\overrightarrow{MB}=\left(2;-1\right)$

Suy ra vectơ pháp tuyến của đường thẳng ∆ là:  $\overrightarrow{n}=\left(1;2\right)$

Do đó phương trình đường thẳng  là: x – 2 + 2(y – 3) = 0 ⇔ x + 2y – 8 = 0

TH2: ∆  song song với AC.

Vectơ chỉ phương của đường thẳng ∆  là: $\overrightarrow{AC}=\left(8;2\right)$  nên vectơ pháp tuyến của đường thẳng ∆  là:  $\overrightarrow{n}=\left(1;-4\right)$

Phương trình đường thẳng ∆  là: x – 4 – 4(y – 2) = 0 ⇔ x – 4y + 4 = 0.

Giải SBT Toán 10 trang 83 Tập 2

Bài 46 trang 83 SBT Toán 10 Tập 2: Có hai tàu điện ngầm A và B chạy trong nội đô thành phố cùng xuất phát từ hai ga, chuyển động đều theo đường thẳng. Trên màn hình ra đa của trạm điều khiển (được coi như mặt phẳng tọa độ Oxy với đơn vị trên các trục tính theo ki-lô-mét), sau khi xuất phát t (giờ) (t ≥ 0), vị trí của tàu A có tọa độ được xác định bởi công thức $\left\{\begin{array}{c}x=7+36t\\ y=-8+8t\end{array}\right.$  , vị trí của tàu B có tọa độ là (9 + 8t; 5 – 36t)

a) Tính côsin góc giữa hai đường đi của hai tàu A và B.

b) Sau bao lâu kể từ thời điểm xuất phát hai tàu gần nhau nhất?

Lời giải:

a) Tàu A có tọa độ được xác định bởi công thức $\left\{\begin{array}{c}x=7+36t\\ y=-8+8t\end{array}\right.$

nên tàu A di chuyển theo hướng của vectơ  $\overrightarrow{u_1}=\left(36;8\right)$

Vị trí của tàu B có tọa độ là (9 + 8t; 5 – 36t)

Hay tàu B di chuyển theo hướng của vectơ $\overrightarrow{u_2}=\left(8;-36\right)$

Ta thấy $\overrightarrow{u_1}.\overrightarrow{u_2}=36.8+8.\left(-36\right)=0$  nên $\overrightarrow{u_1}$  vuông góc với  $\overrightarrow{u_2}$

Vì vậy hai tàu di chuyển vuông góc với nhau.

b) Vị trí của tàu A sau khi xuất phát t giờ là: M(7 + 36t;  – 8 – 8t)

Vị trí của tàu B sau khi xuất phát t giờ là: N(9 + 8t;  5 – 36t).

Suy ra  $\overrightarrow{MN}=\left(2-28t;13-44t\right)$

 $\begin{array}{l}\Rightarrow MN=\left|\overrightarrow{MN}\right|=\sqrt{{\left(2-28t\right)}^2+{\left(13-44t\right)}^2}\\ =\sqrt{2720{\left(t-\frac{157}{680}\right)}^2+\frac{4761}{170}}\ge \sqrt{\frac{4761}{170}}\approx \mathrm{5,29}km\end{array}$

Vậy MN nhỏ nhất là 5,29km khi t = $\frac{157}{680}$  giờ.

Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác: 

Bài 2: Biểu thức tọa độ của các phép toán vectơ

Bài 3: Phương trình đường thẳng

Bài 5: Phương trình đường tròn

Bài 6: Ba đường conic

Bài tập cuối chương 7