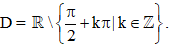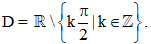Xét tính chẵn, lẻ của các hàm số: a) y = sin 2x; b) y = |sin x|; c) y = tan2 x

Bài 42 trang 23 SBT Toán 11 Tập 1: Xét tính chẵn, lẻ của các hàm số:

a) y = sin 2x;

b) y = |sin x|;

c) y = tan² x;

d) $y=\sqrt{1-\cos x}$ ;

e) y = tan x + cot x;

g) y = sin x . cos 3x.

Trả lời

a) Hàm số y = sin 2x có:

+ Tập xác định: D = ℝ.

+ Với x ∈ ℝ thì – x ∈ ℝ và f(– x) = sin(– 2x) = – sin 2x = – f(x).

Do đó, hàm số y = sin 2x là hàm số lẻ.

b) Hàm số  y = |sin x| có:

+ Tập xác định: D = ℝ.

+ Với x ∈ ℝ thì – x ∈ ℝ và f(– x) = |sin(– x)| = |– sin x| = |sin x| = f(x).

Do đó, hàm số y = |sin x| là hàm số chẵn.

c) Hàm số y = tan² x có:

+ Tập xác định: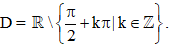 

+ Với x ∈ D thì – x ∈ D và f(– x) = tan² (– x) = (– tan x)² = tan² x = f(x).

Do đó, hàm số y = tan² x là hàm số chẵn.

d) Vì cos x ∈ [− 1; 1] nên 1 – cos x ≥ 0 với mọi x ∈ ℝ.

Hàm số $y=\sqrt{1-\cos x}$  có:

+ Tập xác định: D = ℝ.

+ Với x ∈ ℝ thì – x ∈ ℝ và $f\left(-x\right)=\sqrt{1-\cos \left(-x\right)}=\sqrt{1-\cos x}=f\left(x\right)$ .

Do đó, hàm số $y=\sqrt{1-\cos x}$  là hàm số chẵn.

e) Hàm số y = tan x + cot x có:

+ Tập xác định: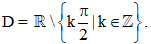 

+ Với x ∈ D thì – x ∈ D và f(– x) = tan(– x) + cot(– x) = – tan x – cot x = – (tan x + cot x) = – f(x).

Do đó, hàm số y = tan x + cot x là hàm số lẻ.

g) Hàm số y = sin x . cos 3x có:

+ Tập xác định: D = ℝ.

+ Với x ∈ ℝ thì – x ∈ ℝ và f(– x) = sin(– x) . cos(– 3x) = – sin x . cos 3x = – f(x).

Do đó, hàm số y = sin x . cos 3x là hàm số lẻ.