Giải SBT Toán 11 (Cánh diều) Bài 1: Dãy số

Giải SBT Toán 11 Bài 1: Dãy số

Bài 1 trang 45 SBT Toán 11 Tập 1: Cho dãy số (u_n) biết u₁ = 2 và $u_n=\frac{u_{n-1}+1}{2}$  với mọi n ≥ 2. Ba số hạng đầu tiên của dãy số lần lượt là:

A. 2; 1; $\frac{3}{2}$ .

B. 2; $\frac{3}{2};\frac{5}{2}$ .

C. 2; $\frac{3}{2};\frac{5}{4}$ .

D. 2;$\frac{3}{2}$ ; 2.

Lời giải:

Đáp án đúng là: C

Ta có: u₁ = 2; $u_2=\frac{u_1+1}{2}=\frac{2+1}{2}=\frac{3}{2}$ ; $u_3=\frac{u_2+1}{2}=\frac{\frac{3}{2}+1}{2}=\frac{5}{4}$ .

Bài 2 trang 45 SBT Toán 11 Tập 1: Cho dãy số (u_n) biết $u_n=\frac{2n^2-1}{n^2+2}$ . Số hạng u₁₀ là:

A. $\frac{19}{12}$ .  

B. $\frac{33}{34}$ .

C. $\frac{199}{102}$ .

D. $\frac{3}{4}$ .

Lời giải:

Đáp án đúng là: C

Ta có $u_{10}=\frac{{2.10}^2-1}{{10}^2+2}=\frac{199}{102}$ .

Bài 3 trang 45 SBT Toán 11 Tập 1: Cho dãy số (u_n) biết $u_n=\frac{n+1}{3n-2}$ . Với $u_k=\frac{8}{19}$  là số hạng của dãy số thì k bằng:

A. 8.

B. 7.

C. 9.

D. 6.

Lời giải:

Đáp án đúng là: B

Giả sử $u_k=\frac{8}{19}$  là một số hạng của dãy số (u_n).

Khi đó k ∈ ℕ^* và $u_k=\frac{k+1}{3k-2}=\frac{8}{19}$ , suy ra 19(k + 1) = 8(3k – 2)

⇔ 19k + 19 = 24k – 16

⇔ 24k – 19k = 19 + 16

⇔ 5k = 35

⇔ k = 7 (t/m).

Vậy k = 7.

Bài 4 trang 45 SBT Toán 11 Tập 1: Cho dãy số (u_n) biết u_n = 3ⁿ. Số hạng u_{n + 1} bằng:

A. 3ⁿ . 3.

B. 3ⁿ + 3.

C. 3ⁿ + 1.

D. 3(n + 1).

Lời giải:

Đáp án đúng là: A

Ta có u_{n + 1} = 3^{n + 1} = 3ⁿ . 3¹ = 3ⁿ . 3.

Bài 5 trang 45 SBT Toán 11 Tập 1: Trong các dãy số (u_n) được xác định như sau, dãy số giảm là:

A. $u_n=\frac{3n-1}{n+1}$ .

B. u_n = n³.

C. $u_n=\frac{1}{3^{n+1}}$ .

D. $u_n=\sqrt{n}$ .

Lời giải:

Đáp án đúng là: C

Xét đáp án C, ta có:

$u_{n+1}-u_n=\frac{1}{3^{n+1+1}}-\frac{1}{3^{n+1}}=\frac{1}{3^{n+2}}-\frac{1}{3^{n+1}}$

              $=\frac{3^{n+1}-3^{n+2}}{3^{n+1}{.3}^{n+2}}=\frac{{3.3}^n-{9.3}^n}{3^{n+1}{.3}^{n+2}}=\frac{-{6.3}^n}{3^{n+1}{.3}^{n+2}}<0$ với mọi n ∈ ℕ^*.

Suy ra u_{n + 1} – u_n < 0, tức là u_{n + 1} < u_n.

Vậy dãy số (u_n) với $u_n=\frac{1}{3^{n+1}}$  là dãy số giảm.

Bài 6 trang 45 SBT Toán 11 Tập 1: Cho dãy số (u_n) biết u_n = cos n. Dãy số (u_n) là:

A. Dãy số tăng.

B. Dãy số giảm.

C. Dãy số bị chặn.  

D. Dãy số bị chặn dưới, không bị chặn trên.

Lời giải:

Đáp án đúng là: C

Ta có – 1 ≤ cos n ≤ 1 với mọi n ∈ ℕ^*.

Do đó, – 1 ≤ u_n ≤ 1 với mọi n ∈ ℕ^*.

Khi đó dãy số (u­_n) bị chặn trên bởi 1 và bị chặn dưới bởi – 1.

Vậy dãy số (u_n) là dãy số bị chặn.

Bài 7 trang 46 SBT Toán 11 Tập 1: Tính tổng 6 số hạng đầu của dãy số (u_n), biết u_n = 3n – 1.

Lời giải:

Ta có u₁ = 3 . 1 – 1 = 2; u₂ = 3 . 2 – 1 = 5;

u₃ = 3 . 3 – 1 = 8; u₄ = 3. 4 – 1 = 11;

u₅ = 3 . 5 – 1 = 14; u₆ = 3 . 6 – 1 = 17.

Do đó, u₁ + u₂ + u₃ + u₄ + u₅ + u₆ = 2 + 5 + 8 + 11 + 14 + 17 = 57.

Vậy tổng 6 số hạng đầu của dãy số (u­_n) là 57. 

Bài 8 trang 46 SBT Toán 11 Tập 1: Cho dãy số (u_n) biết u₁ = 2 và $u_n=\sqrt{2+u_{n-1}^2}$  với mọi n ≥ 2. Viết năm số hạng đầu của dãy số và dự đoán công thức của số hạng tổng quát u_n.

Lời giải:

Năm số hạng đầu của dãy số (u_n) là: u₁ = 2;

$u_2=\sqrt{2+u_1^2}=\sqrt{2+2^2}=\sqrt{6}$;

$u_3=\sqrt{2+u_2^2}=\sqrt{2+{\left(\sqrt{6}\right)}^2}=\sqrt{8}=2\sqrt{2}$;

$u_4=\sqrt{2+u_3^2}=\sqrt{2+{\left(2\sqrt{2}\right)}^2}=\sqrt{10}$;

$u_5=\sqrt{2+u_4^2}=\sqrt{2+{\left(\sqrt{10}\right)}^2}=\sqrt{12}=2\sqrt{3}$.

Ta thấy $2=\sqrt{2.\left(1+1\right)}$ ; $\sqrt{6}=\sqrt{2.\left(2+1\right)}$ ; $\sqrt{8}=\sqrt{2.\left(3+1\right)}$ ;

$\sqrt{10}=\sqrt{2.\left(4+1\right)}$; $\sqrt{12}=\sqrt{2.\left(5+1\right)}$ .

Khi đó dự đoán công thức số hạng tổng quát của dãy số (u_n) là $u_n=\sqrt{2\left(n+1\right)}$ .

Bài 9 trang 46 SBT Toán 11 Tập 1: Trong mặt phẳng toạ độ Oxy, cho hàm số $y=\frac{2x-1}{2x^2+1}$  có đồ thị (C). Với mỗi số nguyên dương n, gọi A_n là giao điểm của đồ thị (C) với đường thẳng x = n. Xét dãy số (u_n), biết u_n là tung độ của điểm A_n. Hãy tìm công thức của số hạng tổng quát u_n.

Lời giải:

Với x = n, ta có $y_n=\frac{2n-1}{2n^2+1}$ , suy ra $A_n\left(n;\frac{2n-1}{2n^2+1}\right)$ .

Vì dãy số (u_n) có u_n là tung độ của điểm A_n, do đó $u_n=\frac{2n-1}{2n^2+1}$ .

Vẫy công thức của số hạng tổng quát là $u_n=\frac{2n-1}{2n^2+1}$ .

Bài 10 trang 46 SBT Toán 11 Tập 1: Cho dãy số (u_n), biết 

a) Viết bốn số hạng đầu của dãy số.

b) Chứng minh rằng u_{n + 4} = u_n với mọi n ≥ 1.

c) Tính tổng 12 số hạng đầu của dãy số.

Lời giải:

a) Bốn số hạng đầu của dãy số (u_n) là:

Vậy u_{n + 4} = u_n với mọi n ≥ 1.

c) Theo câu b) ta có u_{n + 4} = u_n với mọi n ≥ 1.

Do đó, u₁ = u₅ = u₉, u₂ = u₆ = u₁₀, u₃ = u₇ = u₁₁, u₄ = u₈ = u₁₂.

Tổng 12 số hạng đầu của dãy số là:

u₁ + u₂ + u₃ + u₄ + ... + u₁₂ = 3(u₁ + u₂ + u₃ + u₄)

                                        = $3\left(\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}+\frac{-\sqrt{2}}{2}+\frac{-\sqrt{2}}{2}\right)=0$ .   

Bài 11 trang 46 SBT Toán 11 Tập 1: Xét tính tăng, giảm của mỗi dãy số (u_n), biết:

a) u_n = 2n + 3;

b) u_n = 3ⁿ – n;

c) $u_n=\frac{\sqrt{n}}{2^n}$ ;

d) u_n = sin n.  

Lời giải:

a) Ta có u_{n + 1} = 2(n + 1) + 3 = 2n + 5.

Xét u_{n + 1} – u_n = (2n + 5) – (2n + 3) = 2 > 0 với mọi n ∈ ℕ^*.

Do đó, u_{n + 1} > u_n với mọi n ∈ ℕ^*.

Vậy dãy số (u_n) với u_n = 2n + 3 là dãy số tăng.

b) Ta có u_{n + 1} = 3^{n + 1} – (n + 1) = 3 . 3ⁿ – n – 1.

Xét u_{n + 1} – u­_n = (3 . 3ⁿ – n – 1) – (3ⁿ – n) = 3 . 3ⁿ – 3ⁿ – 1 = 2 . 3ⁿ – 1 > 0 với mọi n ∈ ℕ^*.

Do đó, u_{n + 1} > u_n với mọi n ∈ ℕ^*.

Vậy dãy số (u_n) với u­_n = 3ⁿ – n là dãy số tăng.

c) Ta có u_{n + 1} = $\frac{\sqrt{n+1}}{2^{n+1}}$  = $\frac{\sqrt{n+1}}{{2.2}^n}$ .

Xét  $u_{n+1}-u_n=\frac{\sqrt{n+1}}{{2.2}^n}-\frac{\sqrt{n}}{2^n}=\frac{\sqrt{n+1}-2\sqrt{n}}{{2.2}^n}$ $=\frac{\sqrt{n+1}-\sqrt{4n}}{{2.2}^n}$

                      $=\frac{n+1-4n}{{2.2}^n\left(\sqrt{n+1}+\sqrt{4n}\right)}=\frac{-3n+1}{{2.2}^n\left(\sqrt{n+1}+\sqrt{4n}\right)}<0$ với mọi n ∈ ℕ^*.

(do – 3n + 1 < 0, 2ⁿ > 0 và  với mọi n ∈ ℕ^*).

Do vậy, u_{n + 1} < u_n với mọi n ∈ ℕ^*.

Vậy dãy số (u_n) với $u_n=\frac{\sqrt{n}}{2^n}$  là dãy số giảm.

Bài 12 trang 46 SBT Toán 11 Tập 1: Cho dãy số (u_n) biết $u_n=\frac{an+2}{n+1}$  với a là số thực. Tìm a để dãy số (u_n) là dãy số tăng.  

Lời giải:

Ta có $u_{n+1}=\frac{a\left(n+1\right)+2}{n+1+1}=\frac{an+a+2}{n+2}$ .

Xét $u_{n+1}-u_n=\frac{an+a+2}{n+2}-\frac{an+2}{n+1}=\frac{\left(an+a+2\right)\left(n+1\right)-\left(an+2\right)\left(n+2\right)}{\left(n+2\right)\left(n+1\right)}$

$=\frac{a{n}^2+an+an+a+2n+2-a{n}^2-2an-2n-4}{\left(n+2\right)\left(n+1\right)}$ $=\frac{a-2}{\left(n+2\right)\left(n+1\right)}$.

Để dãy số (u_n) là dãy số tăng thì u_{n + 1} > u_n với mọi n ∈ ℕ^* hay u_{n + 1} – u_n > 0 với mọi n ∈ ℕ^*, tức là $\frac{a-2}{\left(n+2\right)\left(n+1\right)}>0$  với mọi n ∈ ℕ^*.

Mà n + 2 > 0, n + 1 > 0 với mọi n ∈ ℕ^*.

Nên $\frac{a-2}{\left(n+2\right)\left(n+1\right)}>0$  ⇔ a – 2 > 0 ⇔ a > 2.

Vậy (u_n) là dãy số tăng khi a > 2.

Bài 13 trang 46 SBT Toán 11 Tập 1: Chứng minh rằng:

a) Dãy số (u_n) với $u_n=\sqrt{n^2+1}$  bị chặn dưới;

b) Dãy số (u­_n) với u_n = – n² – n bị chặn trên;  

c) Dãy số (u_n) với $u_n=\frac{2n+1}{n+2}$  bị chặn. 

Lời giải:

a) Ta có n² ≥ 1 với mọi n ∈ ℕ^*.

Do đó, $\sqrt{n^2+1}\ge \sqrt{1+1}=\sqrt{2}$  với mọi n ∈ ℕ^*.

Vậy dãy số (u_n) với $u_n=\sqrt{n^2+1}$  bị chặn dưới.

b) Ta có – n² – n ≤ – 2 với mọi n ∈ ℕ^*.

Do đó, dãy số (u_n) với u_n = – n² – n bị chặn trên.

c) Ta có $\frac{2n+1}{n+2}>0$  với mọi n ∈ ℕ^*. Do đó, dãy số (u_n) với $u_n=\frac{2n+1}{n+2}$  bị chặn dưới. (1)

Lại có $\frac{2n+1}{n+2}=\frac{2\left(n+2\right)-3}{n+2}=2-\frac{3}{n+2}<2$  với mọi n ∈ ℕ^*.

Do đó, dãy số (u_n) với $u_n=\frac{2n+1}{n+2}$  bị chặn trên. (2)

Từ (1) và (2), suy ra dãy số (u_n) với $u_n=\frac{2n+1}{n+2}$  bị chặn. 

Bài 14 trang 46 SBT Toán 11 Tập 1: Với mỗi số nguyên dương n, lấy n + 6 điểm cách đều nhau trên đường tròn. Nối mỗi điểm với điểm cách nó hai điểm trên đường tròn đó để tạo thành các ngôi sao như Hình 1. Gọi u_n là số đo góc ở đỉnh tính theo đơn vị độ của mỗi ngôi sao thì ta được dãy số (u_n). Tìm công thức của số hạng tổng quát u_n.

Lời giải:

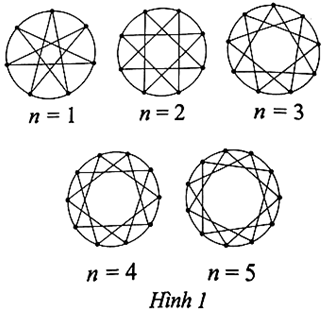
Ta thấy đường tròn được chia thành n + 6 cung bằng nhau và mỗi cung có số đo bằng $\left(\frac{360}{n+6}\right)\begin{array}{c}°\end{array}$ . Do mỗi điểm được nối với điểm cách nó hai điểm trên đường tròn nên góc ở đỉnh của mỗi ngôi sao là góc nội tiếp chắn n + 6 – 2 . 3 = n cung bằng nhau đó. Suy ra số đo góc ở đỉnh tính theo đơn vị độ của mỗi ngôi sao là $u_n=\frac{1}{2}.\frac{360}{n+6}.n=\frac{180n}{n+6}$ .

Xem thêm lời giải bài tập SBT Toán 11 Cánh diều hay, chi tiết khác:

Bài 4: Phương trình lượng giác cơ bản

Bài tập cuối chương 1

Bài 2: Cấp số cộng

Bài 3: Cấp số nhân

Bài tập cuối chương 2