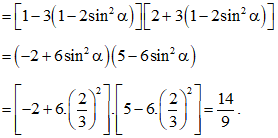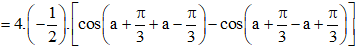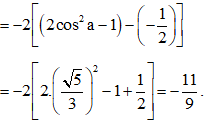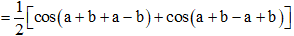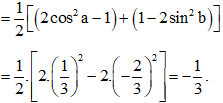Giải SBT Toán 11 Bài 2: Các phép biến đổi lượng giác
Bài 15 trang 14 SBT Toán 11 Tập 1: Cho hai góc a và b với tan a = và tanb = Khi đó, tan(a + b) bằng:
A. 1.
B. .
C. .
D. – 1.
Lời giải:
Đáp án đúng là: A
Ta có .
Bài 16 trang 14 SBT Toán 11 Tập 1: Nếu với thì giá trị của bằng:
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: A
Vì nên cos α > 0, do đó từ sin2 α + cos2 α = 1, suy ra
.
Ta có .
Bài 17 trang 14 SBT Toán 11 Tập 1: Nếu thì giá trị của biểu thức bằng:
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: D
Ta có
Bài 18 trang 15 SBT Toán 11 Tập 1: Chọn đẳng thức đúng trong các đẳng thức sau:
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: B
Ta có sin4 x + cos4 x = 1 – 2sin2 x cos2 x (theo Bài 9a)
= 1 – 2 (sin x cos x)2 =
.
Vậy .
A. – 2cos x.
B. – cos x.
C. 0.
D. sin x – cos x.
Lời giải:
Đáp án đúng là: A
Ta có cos(120° – x) + cos(120° + x) – cos x
= cos 120° cos x + sin 120° sin x + cos 120° cos x – sin 120° sin x – cos x
= 2 cos 120° cos x – cos x
= 2 . . cos x – cos x
= – cos x – cos x
= – 2 cos x.
Bài 20 trang 15 SBT Toán 11 Tập 1: Nếu thì giá trị của bằng:
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: B
Ta có .
Bài 21 trang 15 SBT Toán 11 Tập 1: Nếu thì giá trị của biểu thức bằng:
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: A
Ta có
Bài 22 trang 15 SBT Toán 11 Tập 1: Nếu thì giá trị cos(a + b) cos(a − b) bằng:
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: D
Ta có cos(a + b) cos(a − b)
Bài 23 trang 15 SBT Toán 11 Tập 1: Giá trị của biểu thức bằng:
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: C
Ta có
.
Bài 24 trang 15 SBT Toán 11 Tập 1: Rút gọn biểu thức ta được kết quả là:
A. tan x.
B. tan 3x.
C. tan 2x.
D. tan x + tan 2x + tan 3x.
Lời giải:
Đáp án đúng là: C
Ta có
.
Bài 25 trang 15 SBT Toán 11 Tập 1: Cho với . Tính:
a) cos a, tan a;
b) ;
c) sin 2a, cos 2a.
Lời giải:
a) Vì nên cos a < 0, do đó từ sin2 a + cos2 a = 1, suy ra
.
Ta có .
b) .
.
.
c) .
.
Bài 26 trang 15 SBT Toán 11 Tập 1: Cho cos a = 0,2 với π < a < 2π. Tính , , .
Lời giải:
Do π < a < 2π nên . Suy ra .
Ta có: , suy ra .
Do đó, .
.
Bài 27 trang 15 SBT Toán 11 Tập 1: Cho . Tính sin a, cos a, tan a.
Lời giải:
Ta có (do )
.
.
.
Bài 28 trang 16 SBT Toán 11 Tập 1: Cho cos(a + 2b) = 2cos a. Chứng minh rằng: tan(a + b) tan b = .
Lời giải:
Ta có cos(a + 2b) = 2cos a
⇔ cos[(a + b) + b] = 2cos[(a + b) – b]
⇔ cos(a + b) . cos b – sin(a + b) . sin b = 2[cos(a + b) . cos b + sin(a + b) . sin b]
⇔ cos(a + b) . cos b – 2 cos(a + b) . cos b = 2 sin(a + b) . sin b + sin(a + b) . sin b
⇔ – cos(a + b) . cos b = 3 sin(a + b) . sin b
⇔ sin(a + b) . sin b = cos(a + b) . cos b
⇔ tan(a + b) tan b = .
Bài 29 trang 16 SBT Toán 11 Tập 1: Cho tam giác ABC, chứng minh rằng:
a) tan A + tan B + tan C = tan A . tan B . tan C (với điều kiện tam giác ABC không vuông);
b) .
Lời giải:
a) Vì tam giác ABC không vuông nên A, B, C khác , do đó tan A, tan B, tan C xác định.
Do A + B + C = π nên A + B = π – C, do đó tan(A + B) = tan(π – C) = tan(– C) = – tanC.
Mà .
Khi đó
⇔ tan A + tan B = – tan C . (1 – tan A . tan B)
⇔ tan A + tan B = – tan C + tan A . tan B . tan C
⇔ tan A + tan B + tan C = tan A . tan B . tan C.
b) Ta có , suy ra nên
.
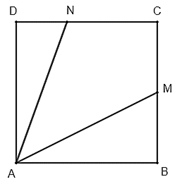
a) Tính .
b) Góc chiếu sáng của đèn pin bằng bao nhiêu độ?
Hình 4
Lời giải:
a) Trong tam giác vuông ABM, có .
Trong tam giác vuông ADN, có .
Do đó, .
b) Từ câu a) ta có = 1 nên .
Suy ra .
Vậy góc chiếu sáng của đèn pin bằng 45°.
Xem thêm lời giải bài tập SBT Toán 11 Cánh diều hay, chi tiết khác:
Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác
Bài 3: Hàm số lượng giác và đồ thị