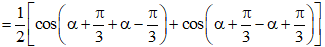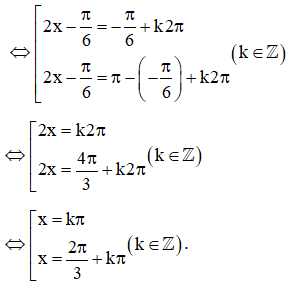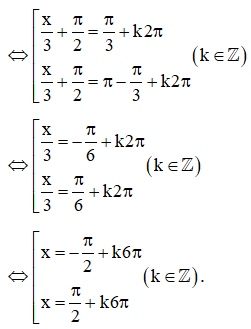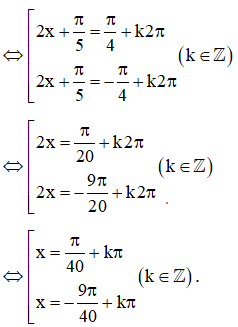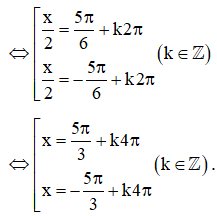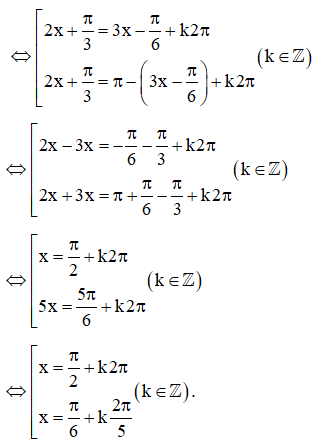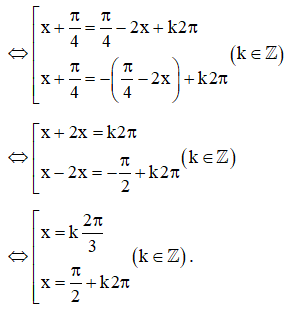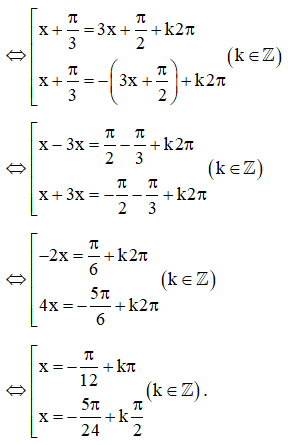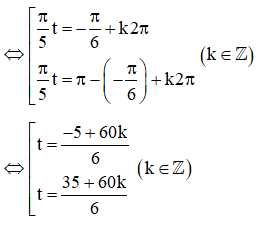Giải SBT Toán 11 (Cánh diều) Bài tập cuối chương 1

Giải SBT Toán 11 Bài tập cuối chương 1

Bài 63 trang 31 SBT Toán 11 Tập 1: Cho lục giác đều ABCDEF nội tiếp trong đường tròn lượng giác (thứ tự đi từ A đến các đỉnh theo chiều dương). Khi đó, số đo của góc lượng giác (OA, OC) bằng:

A. $\frac{2\pi }{3}+k2\pi$ .

B. $-\frac{2\pi }{3}+k2\pi$ .

C. $\frac{\pi }{3}+k2\pi$ .

D. $-\frac{\pi }{3}+k2\pi$ .

Lời giải:

Đáp án đúng là: A

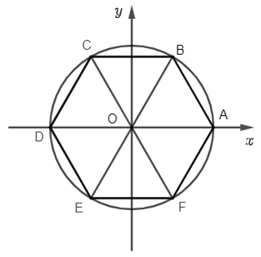
Vì ABCDEF là lục giác đều nên

$\widehat{AOB}=\widehat{BOC}=\widehat{COD}=\widehat{DOE}=\widehat{EOF}=\widehat{FOA}=\frac{360°}{6}=60°=\frac{\pi }{3}$.

Khi đó, ta có: $\left(OA,OC\right)=\frac{\pi }{3}+\frac{\pi }{3}+k2\pi =\frac{2\pi }{3}+k2\pi$ .

Bài 64 trang 31 SBT Toán 11 Tập 1: Cho tan α = 2. Giá trị của biểu thức $A=\frac{3\sin \alpha +\cos \alpha }{\sin \alpha -\cos \alpha }$  bằng:

Lời giải:

Vì tan α = 2 xác định nên cos α ≠ 0. Chia cả tử và mẫu của A cho cos α ta được:

$A=\frac{3\sin \alpha +\cos \alpha }{\sin \alpha -\cos \alpha }$$=\frac{3\tan \alpha +1}{\tan \alpha -1}=\frac{3.2+1}{2-1}=\frac{7}{1}=7$.

Bài 65 trang 32 SBT Toán 11 Tập 1: Giá trị của biểu thức A = (2sin x – cos x)² + (2cos x + sin x)² bằng:

A. 5.

B. 3.

C. 4.

D. 2.  

Lời giải:

Đáp án đúng là: A

Ta có A = (2sin x – cos x)² + (2cos x + sin x)²

= 4sin² x – 4sin x cos x + cos² x + 4cos² x + 4cos x sin x + sin² x

= 5sin² x + 5cos² x

= 5(sin² x + cos² x)

= 5 . 1 = 5.

Bài 66 trang 32 SBT Toán 11 Tập 1: Nếu hai góc a và b có tan a = $\frac{1}{3}$  và tan b = $\frac{1}{2}$  thì giá trị của tan(a – b) bằng:

A. $\frac{1}{7}$ .

B. $-\frac{1}{5}$ .

C. $-\frac{1}{7}$ .

D. 1.

Lời giải:

Đáp án đúng là: C

Ta có $\tan \left(a-b\right)=\frac{\tan a-\tan b}{1+\tan a\tan b}=\frac{\frac{1}{3}-\frac{1}{2}}{1+\frac{1}{3}.\frac{1}{2}}=\frac{-\frac{1}{6}}{\frac{7}{6}}=-\frac{1}{7}$ .

Bài 67 trang 32 SBT Toán 11 Tập 1: Nếu $\cos 2\alpha =\frac{\sqrt{3}}{6}$  thì giá trị của biểu thức $\cos \left(\alpha +\frac{\pi }{3}\right)\cos \left(\alpha -\frac{\pi }{3}\right)$  bằng:

A. $\frac{\sqrt{3}}{3}$ .

B. $\frac{-3+\sqrt{3}}{12}$ .

C. $-\frac{\sqrt{3}}{3}$ .

D. $\frac{3+\sqrt{3}}{12}$ .

Lời giải:

Đáp án đúng là: B

Ta có $\cos \left(\alpha +\frac{\pi }{3}\right)\cos \left(\alpha -\frac{\pi }{3}\right)$

$=\frac{1}{2}\left(\cos 2\alpha +\cos \frac{2\pi }{3}\right)$

$=\frac{1}{2}\left(\frac{\sqrt{3}}{6}-\frac{1}{2}\right)=\frac{-3+\sqrt{3}}{12}$.

Bài 68 trang 32 SBT Toán 11 Tập 1: Phương trình cos 2x = 0 có các nghiệm là:

A. $x=\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$ .

B. $x=\frac{\pi }{4}+k\pi \left(k\in \mathbb{Z}\right)$ .

C. $x=\frac{\pi }{4}+k\frac{\pi }{2}\left(k\in \mathbb{Z}\right)$ .

D. $x=k\pi \left(k\in \mathbb{Z}\right)$ .

Lời giải:

Đáp án đúng là: C

Ta có cos 2x = 0 $\iff 2x=\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$ $\iff x=\frac{\pi }{4}+k\frac{\pi }{2}\left(k\in \mathbb{Z}\right)$  .

Bài 69 trang 32 SBT Toán 11 Tập 1: Phương trình tan x = $-\frac{1}{\sqrt{3}}$ có các nghiệm là: 

A. $x=\frac{\pi }{6}+k\pi \left(k\in \mathbb{Z}\right)$ .

B. $x=-\frac{\pi }{6}+k\pi \left(k\in \mathbb{Z}\right)$ .

C. $x=\frac{\pi }{3}+k\pi \left(k\in \mathbb{Z}\right)$ .

D. $x=-\frac{\pi }{3}+k\pi \left(k\in \mathbb{Z}\right)$.

Lời giải:

Đáp án đúng là: B

Do $\tan \left(-\frac{\pi }{6}\right)=-\frac{1}{\sqrt{3}}$  nên tan x = $-\frac{1}{\sqrt{3}}$ $\iff \tan x=\tan \left(-\frac{\pi }{6}\right)$

$\iff x=-\frac{\pi }{6}+k\pi \left(k\in \mathbb{Z}\right)$.

Bài 70 trang 32 SBT Toán 11 Tập 1: Chứng minh mỗi đẳng thức sau là đúng:

a) sin 45° . cos 30° + cos(– 45°) . sin(– 30°) = sin 15°;

b) $\tan \frac{9\pi }{20}=\frac{1+\tan \frac{\pi }{5}}{1-\tan \frac{\pi }{5}}$ .

Lời giải:

a) Ta có VT = sin 45° . cos 30° + cos(– 45°) . sin(– 30°)

                   = sin 45° . cos 30° + cos 45° . (– sin 30°)

= sin 45° . cos 30° – cos 45° . sin 30°

= sin(45° – 30°)

= sin 15° = VP  (đpcm).

b) Ta có $\tan \frac{9\pi }{20}=\tan \left(\frac{\pi }{4}+\frac{\pi }{5}\right)=\frac{\tan \frac{\pi }{4}+\tan \frac{\pi }{5}}{1-\tan \frac{\pi }{4}.\tan \frac{\pi }{5}}=\frac{1+\tan \frac{\pi }{5}}{1-\tan \frac{\pi }{5}}$.

Vậy $\tan \frac{9\pi }{20}=\frac{1+\tan \frac{\pi }{5}}{1-\tan \frac{\pi }{5}}$  (đpcm).

Bài 71 trang 32 SBT Toán 11 Tập 1: Cho sin(45°– α) = $\frac{1}{2\sqrt{2}}$ .

a) Chứng minh rằng ${\sin }^2\left(45°-\alpha \right)=\frac{1-\sin 2\alpha }{2}$ .

b) Tính sin 2α.

Lời giải:

a) Sử dụng công thức hạ bậc và quan hệ lượng giác của hai góc phụ nhau, ta có:

${\sin }^2\left(45°-\alpha \right)=\frac{1-\cos \left(90°-2\alpha \right)}{2}=\frac{1-\sin 2\alpha }{2}$.

Vậy ${\sin }^2\left(45°-\alpha \right)=\frac{1-\sin 2\alpha }{2}$ (đpcm).

b) Vì sin(45°– α) = $\frac{1}{2\sqrt{2}}$  nên sin²(45°– α) = ${\left(\frac{1}{2\sqrt{2}}\right)}^2=\frac{1}{8}$ .

Theo câu a) ta có ${\sin }^2\left(45°-\alpha \right)=\frac{1-\sin 2\alpha }{2}$ , do đó $\frac{1-\sin 2\alpha }{2}=\frac{1}{8}$ .

Từ đó suy ra $\sin 2\alpha =\frac{3}{4}$ .

Bài 72 trang 32 SBT Toán 11 Tập 1: Giải phương trình:

a) $\sin \left(2x-\frac{\pi }{6}\right)=-\frac{1}{2}$ ;

b) $\sin \left(\frac{x}{3}+\frac{\pi }{2}\right)=\frac{\sqrt{3}}{2}$ ;

c) $\cos \left(2x+\frac{\pi }{5}\right)=\frac{\sqrt{2}}{2}$ ;

d) $2\cos \frac{x}{2}+\sqrt{3}=0$ ;

e) $\sqrt{3}\tan \left(2x+\frac{\pi }{3}\right)-1=0$ ;

g) cot(3x + π) = – 1.

Lời giải:

a) Do $\sin \left(-\frac{\pi }{6}\right)=-\frac{1}{2}$  nên $\sin \left(2x-\frac{\pi }{6}\right)=-\frac{1}{2}$ $\iff \sin \left(2x-\frac{\pi }{6}\right)=\sin \left(-\frac{\pi }{6}\right)$

b) Do $\sin \frac{\pi }{3}=\frac{\sqrt{3}}{2}$  nên $\sin \left(\frac{x}{3}+\frac{\pi }{2}\right)=\frac{\sqrt{3}}{2}$ $\iff \sin \left(\frac{x}{3}+\frac{\pi }{2}\right)=\sin \frac{\pi }{3}$

c) Do $\cos \frac{\pi }{4}=\frac{\sqrt{2}}{2}$  nên  $\cos \left(2x+\frac{\pi }{5}\right)=\frac{\sqrt{2}}{2}$ $\iff \cos \left(2x+\frac{\pi }{5}\right)=\cos \frac{\pi }{4}$

d) $2\cos \frac{x}{2}+\sqrt{3}=0$

$\iff \cos \frac{x}{2}=-\frac{\sqrt{3}}{2}$

  $\iff \cos \frac{x}{2}=\cos \frac{5\pi }{6}$    (do $\cos \frac{5\pi }{6}=-\frac{\sqrt{3}}{2}$ )

e) $\sqrt{3}\tan \left(2x+\frac{\pi }{3}\right)-1=0$

$\iff \tan \left(2x+\frac{\pi }{3}\right)=\frac{1}{\sqrt{3}}$

$\iff \tan \left(2x+\frac{\pi }{3}\right)=\tan \frac{\pi }{6}$            (do $\tan \frac{\pi }{6}=\frac{1}{\sqrt{3}}$ )

$\iff 2x+\frac{\pi }{3}=\frac{\pi }{6}+k\pi \left(k\in \mathbb{Z}\right)$

$\iff 2x=-\frac{\pi }{6}+k\pi \left(k\in \mathbb{Z}\right)$

$\iff x=-\frac{\pi }{12}+k\frac{\pi }{2}\left(k\in \mathbb{Z}\right)$.

g) Do $\cot \left(-\frac{\pi }{4}\right)=-1$  nên cot(3x + π) = – 1 $\iff \cot \left(3x+\pi \right)=\cot \left(-\frac{\pi }{4}\right)$

$\iff 3x+\pi =-\frac{\pi }{4}+k\pi \left(k\in \mathbb{Z}\right)$

$\iff 3x=-\frac{5\pi }{4}+k\pi \left(k\in \mathbb{Z}\right)$

$\iff x=-\frac{5\pi }{12}+k\frac{\pi }{3}\left(k\in \mathbb{Z}\right)$.

Bài 73 trang 33 SBT Toán 11 Tập 1: Giải phương trình:

a) $\sin \left(2x+\frac{\pi }{3}\right)=\sin \left(3x-\frac{\pi }{6}\right)$ ;

b) $\cos \left(x+\frac{\pi }{4}\right)=\cos \left(\frac{\pi }{4}-2x\right)$ ;

c) ${\cos }^2\left(\frac{x}{2}+\frac{\pi }{6}\right)={\cos }^2\left(\frac{3x}{2}+\frac{\pi }{4}\right)$ ;

d) $\cot 3x=\tan \frac{2\pi }{7}$ .

Lời giải:

a) $\sin \left(2x+\frac{\pi }{3}\right)=\sin \left(3x-\frac{\pi }{6}\right)$

b) $\cos \left(x+\frac{\pi }{4}\right)=\cos \left(\frac{\pi }{4}-2x\right)$

c) Sử dụng công thức hạ bậc ta có:

${\cos }^2\left(\frac{x}{2}+\frac{\pi }{6}\right)={\cos }^2\left(\frac{3x}{2}+\frac{\pi }{4}\right)$

$\iff \frac{1+\cos \left(x+\frac{\pi }{3}\right)}{2}=\frac{1+\cos \left(3x+\frac{\pi }{2}\right)}{2}$

$\iff \cos \left(x+\frac{\pi }{3}\right)=\cos \left(3x+\frac{\pi }{2}\right)$

d) Sử dụng quan hệ phụ nhau của hai góc lượng giác, ta có:

$\cot 3x=\tan \frac{2\pi }{7}$

$\iff \cot 3x=\cot \left(\frac{\pi }{2}-\frac{2\pi }{7}\right)$

$\iff \cot 3x=\cot \frac{3\pi }{14}$

$\iff 3x=\frac{3\pi }{14}+k\pi \left(k\in \mathbb{Z}\right)$

$\iff x=\frac{\pi }{14}+k\frac{\pi }{3}\left(k\in \mathbb{Z}\right)$.

Bài 74 trang 33 SBT Toán 11 Tập 1: Một chất điểm chuyển động đều theo chiều ngược chiều kim đồng hồ trên đường tròn bán kính 5 cm. Khoảng cách h (cm) từ chất điểm đến trục hoành được tính theo công thức h = |y|, trong đó $y=a\sin \left(\frac{\pi }{5}t\right)$  với t là thời gian chuyển động của chất điểm tính bằng giây (t ≥ 0) và chất điểm bắt đầu chuyển động từ vị trí A (Hình 16).

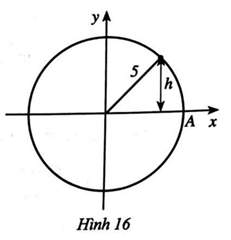
a) Chất điểm chuyển động một vòng hết bao nhiêu giây?

b) Tìm giá trị của a.

c) Tìm thời điểm sao cho chất điểm ở vị trí có h = 2,5 cm và nằm phía dưới trục hoành trong một vòng quay đầu tiên.

Lời giải:

a) Xét h = 0 hay |y| = 0, suy ra y = 0, tức là $a\sin \left(\frac{\pi }{5}t\right)=0$ $\iff \sin \left(\frac{\pi }{5}t\right)=0$

$\iff \frac{\pi }{5}t=k\pi \left(k\in \mathbb{Z}\right)$ $\iff t=5k\left(k\in \mathbb{Z},k\ge 0\right)$ (do t ≥ 0).

Ta nhận thấy, từ thời điểm ban đầu, cứ sau 5 giây, khoảng cách từ chất điểm đến trục hoành lại bằng 0. Suy ra sau mỗi 5 giây, chất điểm chuyển động được nửa vòng. Vậy chất điểm chuyển động một vòng hết 10 giây.

b) Do chất điểm chuyển động một vòng hết 10 giây nên khi t = 2,5 giây thì chất điểm chuyển động được một phần tư vòng theo chiều dương, suy ra tại t = 2,5 ta có y = |y| = h = 5 (do bằng bán kính). Khi đó, $a\sin \left(\frac{\pi }{5}\mathrm{.2,5}\right)=5$ $\iff a=5$.

Vậy a = 5.

c) Từ kết quả câu b, ta có: $y=5\sin \left(\frac{\pi }{5}t\right)$.

Do h = 2,5 cm và chất điểm nằm ở dưới trục hoành nên y = – 2,5.

Với y = – 2,5, ta có: $5\sin \left(\frac{\pi }{5}t\right)=-\mathrm{2,5}$

$\iff \sin \left(\frac{\pi }{5}t\right)=-\frac{1}{2}$

$\iff \sin \left(\frac{\pi }{5}t\right)=\sin \left(-\frac{\pi }{6}\right)$

Với vòng quay đầu tiên thì 0 ≤ t ≤ 10, do đó $t=\frac{35}{6},t=\frac{55}{6}$ .

Vậy tại thời điểm $t=\frac{35}{6}$  giây, $t=\frac{55}{6}$  giây thì chất điểm ở vị trí có h = 2,5 cm và nằm ở dưới trục hoành trong một vòng quay đầu tiên.

Xem thêm lời giải bài tập SBT Toán 11 Cánh diều hay, chi tiết khác:

Bài 3: Hàm số lượng giác và đồ thị

Bài 4: Phương trình lượng giác cơ bản

Bài 1: Dãy số

Bài 2: Cấp số cộng

Bài 3: Cấp số nhân