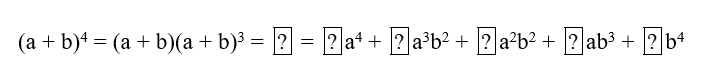Xét công thức khai triển (a + b)^3 = a^3 + 3(a^2) b + 3ab^2 + b^3

Hoạt động khám phá trang 33 Toán lớp 10 Tập 2: a) Xét công thức khai triển (a + b)³ = a³ + 3a²b + 3ab² + b³.

i) Liệt kê các số hạng của khai triển trên.

ii) Liệt kê các hệ số của khai triển trên.

iii) Tính giá trị của $C_3^0;C_3^1;C_3^2;C_3^3$ (có thể sử dụng máy tính) rồi so sánh với các hệ số trên. Có nhận xét gì?

b) Hoàn thành biến đổi sau đây để tìm công thức khai triển của (a + b)⁴:

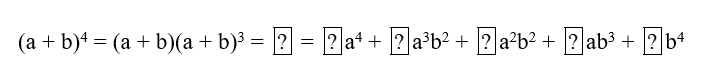
Tính giá trị của $C_4^0,C_4^1,C_4^2,C_4^3,C_4^4$, rồi so sánh với các hệ số của khai triển.

Từ đó, hãy sử dụng các kí hiệu $C_4^0,C_4^1,C_4^2,C_4^3,C_4^4$ để viết lại công thức khai triển trên.

c) Từ kết quả của câu a) và b), hãy dự đoán công thức khai triển của (a + b)⁵. Tính toán để kiểm tra dự đoán đó.

Trả lời

a) Xét công thức khai triển (a + b)³ = a³ + 3a²b + 3ab² + b³, có:

i) Các số hạng của khai triển trên là: a³; 3a²b; 3ab²; b³.

ii) Tương ứng với các số hạng ta có các hệ số xuất hiện trong khai triển trên lần lượt là: 1; 3; 3; 1.

Khi đó ta thấy $C_3^0;C_3^1;C_3^2;C_3^3$ lần lượt bằng hệ số của các số hạng a³; 3a²b; 3ab²; b³ trong khai triển đã cho.

iii) Sử dụng máy tính ta có: $C_3^0=1$, $C_3^1=3$, $C_3^2=3$, $C_3^3=1$.

b) Ta có: (a + b)⁴ = (a + b)(a + b)³

= (a + b)(a³ + 3a²b + 3ab² + b³)

= a⁴ + 3a³b + 3a²b² + ab³ + a³b + 3a²b² + 3ab³ + b⁴

= a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

Bằng cách sử dụng mát tính, giá trị của $C_4^0,C_4^1,C_4^2,C_4^3,C_4^4$ lần lượt là:

$C_4^0=1,C_4^1=4,C_4^2=6,C_4^3=4,C_4^4=1$.

Khi đó ta thấy $C_4^0,C_4^1,C_4^2,C_4^3,C_4^4$ lần lượt bằng hệ số của các số hạng a⁴; 4a³b; 6a²b²; 4ab³; b⁴ trong khai triển đã cho.

Bằng cách sử dụng các kí hiệu $C_4^0,C_4^1,C_4^2,C_4^3,C_4^4$, ta viết lại công thức khai triển trên như sau:

(a + b)⁴ = $C_4^0$a⁴ + $C_4^1$a³b + $C_4^2$a²b² + $C_4^3$ab³ + $C_4^4$b⁴.

c) Từ kết quả câu câu a) và b) ta có dự đoán sau:

(a + b)⁵ = $C_5^0$a⁵b⁰ + $C_5^1$a⁴b¹ + $C_5^2$a³b² + $C_5^3$a²b³ + $C_5^4$ab⁴ + $C_5^5$b⁵

= a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵.

Kiểm tra dự đoán:

(a + b)⁵ = (a + b)³.(a + b)² = (a³ + 3a²b + 3ab² + b³)(a² + 2ab + b²)

= a⁵ + 2a⁴b + a³b² + 3a⁴b + 6a³b² + 3a²b³ + 3a³b² + 6a²b³ + 3ab⁴ + a²b³ + 2ab⁴ + b⁵

= a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵.

Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Quy tắc cộng và quy tắc nhân

Bài 2: Hoán vị, chỉnh hợp và tổ hợp

Bài 3: Nhị thức Newton

Bài tập cuối chương 8

Bài 1: Toạ độ của vectơ

Bài 2: Đường thẳng trong mặt phẳng toạ độ