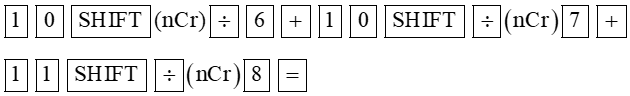Giải SGK Toán 10 (Chân trời sáng tạo) Bài 2: Hoán vị, chỉnh hợp và tổ hợp

Giải Toán 10 Bài 2: Hoán vị, chỉnh hợp và tổ hợp

Hoạt động khởi động trang 26 Toán lớp 10 Tập 2: Có bao nhiêu cách chọn 5 cầu thủ từ 11 cầu thủ? Có bao nhiêu cách sắp xếp 5 cầu thủ đó theo thứ tự để thực hiện đá luân lưu? Bằng cách sử dụng quy tắc nhân, bạn có tìm được câu trả lời?

Học xong bài học này, bạn hãy tìm cách nhanh hơn để trả lời các câu hỏi trên.

Lời giải:

*) Bằng cách sử dụng quy tắc nhân, ta có:

Cách để chọn 5 cầu thủ từ 11 cầu thủ để thực hiện đá luân lưu được chia làm 5 giai đoạn như sau:

+ Giai đoạn thứ nhất: Chọn cho vị trí cầu thủ thứ nhất có 11 cách chọn.

+ Giai đoạn thứ hai: Ứng với cầu thủ thứ nhất, có 10 cách chọn cho vị trí cầu thủ thứ hai.

+ Giai đoạn thứ ba: Ứng với cầu thủ thứ nhất và câu thủ thứ hai, có 9 cách chọn cho vị trí cầu thủ thứ ba.

+ Giai đoạn thứ tư: Ứng với ba cầu thủ đã chọn, có 8 cách chọn cho vị trí cầu thủ thứ tư.

+ Giai đoạn thứ năm: Ứng với bốn cầu thủ đã chọn, có 7 cách chọn cho vị trí cầu thủ thứ tư.

Theo quy tắc nhân ta có: 11.10.9.8.7 = 55 440 cách chọn.

Vậy có 55 440 cách chọn 5 cầu thủ từ 11 cầu thủ để đá luân lưu.

Ngoài ra ta có thể chia công việc chọn 5 cầu thủ từ 11 cầu thủ để đá luân lưu thành hai giai đoạn:

+ Giai đoạn 1: Chọn 5 cầu thủ từ 11 cầu thủ, có x cách chọn.

+ Giai đoạn 2: Ứng với 5 cầu thủ vừa chọn ra, cách xếp 5 cầu thủ đế đá luân lưu là:

- Vị trí đá thứ nhất: có 5 cách chọn.

- Vị trí đá thứ hai: có 4 cách chọn.

- Vị trí đá thứ ba: có 3 cách chọn.

- Vị trí đá thứ 4: có 2 cách chọn.

- Vị trí đá thứ 5: có 1 cách chọn.

Do đó có 5.4.3.2.1 = 120 cách để xếp 5 cầu thủ được chọn ra đá luân lưu.

Áp dụng quy tắc nhân ta có x.120 cách chọn 5 cầu thủ từ 11 cầu thủ để đá luân lưu. Hay ta có x.120 = 55 440.

⇔ x = 55 440 : 120 = 420 cách.

Vậy có 420 cách chọn ra 5 cầu thủ trong 11 cầu thủ.

+) Sau bài học này ta có thể sử dụng công thức sau để giải nhanh hơn:

Số cách chọn 5 cầu thủ từ 11 cầu thủ là tổ hợp chập 5 của 11: $C_{11}^5=$ 420 cách.

Số cách chọn 5 cầu thủ để đá luân lưu: $C_{11}^5$.5! = $A_{11}^5$ = 55 440 cách.

1. Hoán vị

Hoạt động khám phá 1 trang 26 Toán lớp 10 Tập 2: Sau giờ thực hành trải nghiệm, ba đội A, B, C bốc thăm để xác định thứ tự trình bày, thuyết minh về sản phẩm của mỗi đội.

a) Hãy liệt kê tất cả các kết quả bốc thăm có thể xảy ra.

b) Có tất cả bao nhiêu kết quả như vậy? Ngoài các đếm lần lượt từng kết quả, có cách nào tìm nhanh hơn không?

Lời giải:

a) Các kết quả bốc thăm có thể xảy ra là:

Việc thuyết minh về sản phẩm của mỗi đội thì thứ tự trình bày có thể có các kết quả sau:

A – B – C;

A – C – B;

B – A – C;

B – C – A;

C – A – B;

C – B – A.

Vậy các kết quả có thể xảy ra là: {A – B – C; A – C – B; B – A – C; B – C – A; C – A – B; C – B – A}.

b) Có 6 kết quả có thể xảy ra về thứ tự thuyết trình của ba đội A, B, C.

Ngoài việc đếm lần lượt từng kết quả, có cách tìm nhanh hơn đó là sử dụng hoán vị. Mỗi cách xếp ba đội A, B, C theo một thứ tự (hay nói cách khác là đổi thứ tự của ba đội) được gọi là một hoán vị các phần tử đó nên ta có 3! = 6 kết quả có thể xảy ra về thứ tự thuyết trình của ba đội A, B, C.

Thực hành 1 trang 28 Toán lớp 10 Tập 2: Một nhóm bạn gồm sáu thành viên cùng đi xem phim, đã mua sáu vé có ghế ngồi cùng dãy và kế tiếp nhau (như Hình 3). Có bao nhiêu cách sắp xếp chỗ ngồi cho các thành viên của nhóm?

Lời giải:

Sắp xếp chỗ ngồi cho 6 thành viên vào 6 ghế là hoán vị của 6 thành viên. Do đó số cách sắp xếp chỗ ngồi cho các thành viên của nhóm là:

P₆ = 6! = 6.5.4.3.2.1 = 720 cách.

Vậy có tất cả 720 cách xếp chỗ ngồi cho các thành viên của nhóm.

Vận dụng 1 trang 28 Toán lớp 10 Tập 2: Một giải bóng đá có 14 đội bóng tham gia. Có bao nhiêu khả năng về thứ hạng các đội bóng khi mùa giải kết thúc?

Lời giải:

Thứ hàng của 14 đội bóng tham gia mùa giải là hoán vị của 14 đội. Do đó các khả năng về thứ hạng đội bóng khi mùa giải kết thúc là:

P₁₄ = 14! = 14.13.12.11.10.9.8.7.6.5.4.3.2.1 ≈ 8,7.10¹⁰.

Vậy có tất cả 8,7.10¹⁰ khả năng về thứ hạng của các đội bóng khi mùa giải kết thúc.

2. Chỉnh hợp

Hoạt động khám phá 2 trang 28 Toán lớp 10 Tập 2: Tại một trạm quan sát, có sẵn 5 lá cờ màu đỏ, trắng, xanh, vàng và cam (kí hiệu Đ, T, X, V, C). Khi cần báo một tin hiệu, người ta chọn 3 lá cờ và cằm vào ba vị trí có sẵn thành một hàng (xem Hình 4).

a) Hãy chỉ ra ít nhất bốn cách chọn và cắm cờ để báo bốn tín hiệu khác nhau.

b) Bằng cách này, có thể báo nhiều nhất bao nhiêu tín hiệu khác nhau?

Lời giải:

a) Ta có ít nhất bốn cách chọn và cắm cờ để báo bốn tín hiệu khác nhau như sau:

Đ – T – X;

Đ – T – V;

Đ – T – C;

T – X – V.

Có thể có các cách chọn cờ khác để báo tín hiệu khác.

b) Số cách chọn 3 lá cờ từ 5 lá cờ có màu như trên để làm đèn báo tín hiệu được chia làm 3 giai đoạn:

- Giai đoạn thứ nhất: Chọn lá cờ thứ nhất, có 5 cách chọn.

- Giai đoạn thứ hai: Ứng với lá cờ thứ nhất, có 4 cách chọn lá cờ thứ hai.

- Giai đoạn thứ ba: Ứng với hai lá cờ vừa chọn, có 3 cách chọn lá cờ thứ ba.

Theo quy tắc nhân ta có: 5.4.3 = 60 cách chọn ba lá cờ từ 5 lá cờ.

Vậy có thể báo nhiều nhất 60 tín hiệu khác nhau.

Thực hành 2 trang 29 Toán lớp 10 Tập 2: Từ bảy chữ số 1; 2; 3; 4; 5; 6; 7, lập các số có ba chữ số đôi một khác nhau.

a) Có thể lập được bao nhiêu số như vậy?

b) Trong các số đó có bao nhiêu số lẻ?

Lời giải:

a) Cách 1: Gọi số có ba chữ số cần tìm là: $\overline{abc}$, trong đó a, b, c được lấy từ các chữ số đã cho, a ≠ 0 và a, b, c đôi một khác nhau.

Khi đó:

a có 7 cách chọn từ các chữ số đã cho;

b có 6 cách chọn từ các chữ số đã cho;

c có 5 cách chọn từ các chữ số đã cho.

Theo quy tắc nhân ta có 7.6.5 = 210 cách.

Vậy có thể lập được 210 số thỏa mãn yêu cầu bài toán.

Cách 2: Việc chọn ra 3 chữ số trong 7 chữ số và lập thành một số có ba chữ số là chỉnh hợp chập 3 của 7. Do đó số các số có ba chữ số đôi một khác nhau là: $A_7^3=210$ số.

Vậy có thể lập được 210 số thỏa mãn yêu cầu bài toán.

b) Gọi số có ba chữ số cần tìm là: $\overline{xyz}$, trong đó x, y, z được lấy từ các chữ số đã cho, x ≠ 0 và x, y, z đôi một khác nhau.

Vì $\overline{xyz}$ là số lẻ nên z có 4 cách chọn;

Vì y khác z nên y có 6 cách chọn;

Vì x khác z và y nên x có 5 cách chọn;

Theo quy tắc nhân ta có 4.6.5 = 120 cách.

Vậy có thể lập được 120 số thỏa mãn yêu cầu bài toán.

3. Tổ hợp

Hoạt động khám phá 3 trang 29 Toán lớp 10 Tập 2: Lan vừa mua 4 cuốn sách, kí hiệu là A, B, C và D. Bạn ấy dự định chọn ra 3 cuốn về quê đọc trong dịp hè.

a) Hãy liệt kê tất cả các cách Lan có thể chọn 3 cuốn sách từ 4 cuốn sách. Có tất cả bao nhiêu cách?

b) Lan dự định đọc lần lượt từng cuốn. Lan có bao nhiêu cách xếp thự tự 3 cuốn đã chọn?

c) Lan có bao nhiêu cách chọn 3 cuốn sách từ 4 cuốn sách và xếp theo thứ tự để đọc lần lượt từng cuốn một.

Lời giải:

a) Cách cách Lan có thể chọn 3 cuốn sách từ 4 cuốn sách là:

A – B – C;

A – B – D;

A – C – D;

B – C – D.

Vậy có tất cả 4 cách chọn 3 cuốn sách từ 4 cuốn sách.

b) Tương ứng với ba cuốn sách được chọn, việc sắp thứ tự của ba cuốn sách này là hoán vị của ba cuốn sách. Do đó số cách xếp thự tự 3 cuốn đã chọn là:

P3 = 3! = 3.2.1 = 6 (cách).

Vậy có tất cả 6 cách xếp thứ tự 3 cuốn đã chọn.

c) Số cách chọn 3 cuốn sách từ 4 cuốn sách và xếp theo thứ tự để đọc lần lượt từng cuốn một là 4.6 = 24 cách.

Vậy Lan có 24 cách để chọn 3 cuốn sách từ 4 cuốn sách và xếp theo thứ tự để đọc lần lượt từng cuốn một.

Thực hành 3 trang 31 Toán lớp 10 Tập 2: Tính:

a) $C_7^2$;

b) $C_9^0+C_9^9$;

c) $C_{15}^3-C_{14}^3$.

Lời giải:

a) $C_7^2=\frac{7!}{2!\left(7-2\right)!}=\frac{\mathrm{7.6.5.4.3.2.1}}{\mathrm{2.1.5.4.3.2.1}}=\frac{7.6}{2.1}=21.$

b) $C_9^0+C_9^9=\frac{9!}{0!.(9-0)!}+\frac{9!}{9!.(9-9)!}=1+1=2$.

c) $C_{15}^3-C_{14}^3=\frac{15!}{3!.\left(15-3\right)!}-\frac{14!}{3!.\left(14-3\right)!}=\frac{15!}{3!.12!}-\frac{14!}{3!.11!}=\frac{\mathrm{15.14.13}}{\mathrm{3.2.1}}-\frac{\mathrm{14.13.12}}{\mathrm{3.2.1}}=91$.

Thực hành 4 trang 31 Toán lớp 10 Tập 2: Nội dung thi đấu đôi nam nữ của giải bóng bàn cấp trường có 7 đội tham gia. Các đội thi đấu vòng tròn một lượt.

a) Nội dung này có tất cả bao nhiêu trận đấu?

b) Sau giải đấu, ba đội có thành tích tốt nhất sẽ được chọn đi thi đấu liên trường. Có bao nhiêu khả năng có thể xảy ra về ba đội được chọn đi thi đấu cấp liên trường?

Lời giải:

a)

Cách 1: Có tất cả 7 đội tham gia và các đội thi đấu vòng tròn một lượt nên một đội sẽ thi đấu với 6 đội còn lại.

Đội 1 sẽ có 6 trận với 6 đội còn lại;

Đội 2 ngoài trận với đội 1 sẽ có thêm 5 trận với 5 đội còn lại;

Đội 3 ngoài trận với đội 1,2 sẽ có thêm 4 trận với 4 đội còn lại;

Đội 4 ngoài trận với đội 1, 2 và 3 sẽ có thêm 3 trận với 3 đội còn lại;

Đội 5 ngoài trận với đội 1, 2, 3 và 4 sẽ có thêm 2 trận với 2 đội còn lại;

Đội 6 ngoài trận với 5 đội trên sẽ có 1 trận với 1 đội còn lại.

Đội 7 đã thi đấu với tất cả 6 đội trên

Theo quy tắc cộng có 6 + 5 + 4 + 3 + 2 + 1 = 21 trận.

Vậy nội dung này có tất cả 21 trận đấu.

Cách 2: Các đội thi đấu vòng tròn từng đôi một nghĩa là số trận đấu giữa 7 đội tham gia là cách chọn ra 2 đội trong 7 đội. Do đó số trận đấu là tổ hợp chập 2 của 7:

$C_7^2=21$ (trận).

b) Việc chọn ra ba đội có thành tích tốt nhất đi thi đấu cấp liên trường là tổ hợp chập 3 của 7. Do đó số khả năng có thể xảy ra về ba đội được chọn thi đấu cấp liên trường là:

$C_7^3=35$ cách.

Vậy có tất cả 35 khả năng có thể xảy ra về ba đội được chọn thi đấu cấp liên trường.

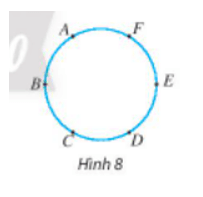
Vận dụng 2 trang 31 Toán lớp 10 Tập 2: Cho 6 điểm cùng nằm trên một đường tròn như Hình 8.

a) Có bao nhiêu đoạn thẳng có điểm đầu mút thuộc các điểm đã cho?

b) Có bao nhiêu tam giác có đỉnh thuộc các điểm đã cho?

Lời giải:

a) Số đoạn thẳng có điểm đầu mút thuộc các điểm đã cho là việc chọn ra 2 điểm từ 6 điểm đã cho hay chính là tổ hợp chập 2 của 6. Do đó số đoạn thẳng có điểm đầu mút thuộc các điểm đã cho là: $C_6^2=15$(đoạn thẳng).

Vậy có tất cả 15 đoạn thẳng có điểm đầu mút thuộc vào các điểm đã cho.

b) Vì trong 6 điểm không có 3 điểm thẳng hàng nên số tam giác có đỉnh thuộc các điểm đã cho là việc chọn ra 3 điểm từ 6 điểm đã cho hay chính là tổ hợp chập 3 của 6. Do đó số tam giác có đỉnh thuộc các điểm đã cho là: $C_6^3=20$(tam giác).

Vậy có tất cả 20 tam giác có đỉnh thuộc các điểm đã cho.

4. Tính số các hoán vị, chỉnh hợp, tổ hợp bằng máy tính cầm tay

Thực hành 5 trang 32 Toán lớp 10 Tập 2: Sử dụng máy tính cầm tay, tính giá trị các biểu thức sau:

a) $A_{15}^{10}$;

b) $C_{10}^6+C_{10}^7+C_{10}^8$;

c) $C_5^1.C_{20}^2+C_5^2.C_{20}^2$.

Lời giải:

a) Để tính $A_{15}^{10}$, ta ấn liên tiếp các phím:

Thì nhận được kết quả là: 1,08972864.10¹⁰.

Vậy $A_{15}^{10}$ ≈ 1,08972864.10¹⁰.

b) Để tính $C_{10}^6+C_{10}^7+C_{10}^8$, ta ấn liên tiếp các phím:

Thì nhận được kết quả là: 495.

c) $C_5^1.C_{20}^2+C_5^2.C_{20}^2$, ta ấn liên tiếp các phím:

Thì ta nhận được kết quả là: 1 150.

Bài tập

Bài 1 trang 32 Toán lớp 10 Tập 2: Cần sắp xếp một nhóm 5 học sinh ngồi vào một dãy 5 chiếc ghế.

a) Có bao nhiêu cách xếp?

b) Nếu bạn Nga (một thành viên trong nhóm) nhất định muốn ngồi vào chiếc ghế ngoài cùng bên trái, thì có bao nhiêu cách xếp?

Lời giải:

a) Sắp xếp 5 học sinh vào 5 ghế là hoán vị của 5 học sinh. Do đó số cách xếp 5 bạn học sinh vào 5 chiếc ghế là: P₅ = 5! = 5.4.3.2.1 = 120 (cách).

Vậy có tất cả 120 cách xếp một nhóm 5 học sinh ngồi vào một dãy 5 chiếc ghế.

b) Nếu bạn Nga ngồi một ghế ngoài cùng bên trái thì còn lại cần xếp 4 bạn học sinh còn lại vào 4 chiếc ghế con lại là hoán vị của 4 học sinh. Do đó số cách xếp 4 bạn học sinh vào 4 chiếc ghế là: P₄ = 4! = 4.3.2.1 = 24 (cách).

Vậy có tất cả 24 cách xếp một nhóm 5 học sinh ngồi vào một dãy 5 chiếc ghế trong đói Nga ngồi chiếc ghế ngoài cùng bên trái.

Bài 2 trang 32 Toán lớp 10 Tập 2: Từ các chữ số sau đây, có thể lập được bao nhiêu số tự nhiên có bốn chữ số khác nhau?

a) 1; 2; 3; 4; 5; 6.

b) 0; 1; 2; 3; 4; 5.

Lời giải:

a) Việc lập số tự nhiên có bốn chữ số khác nhau từ 6 chữ số đã cho là chỉnh hợp chập 4 của 6. Do đó số số tự nhiên có bốn chữ số khác nhau là: $A_6^4=360$(số).

Vậy có tất cả 360 số tự nhiên có bốn chữ số khác nhau được lập từ các chữ số đã cho.

b) Gọi số cần tìm có dạng $\overline{abcd}$, trong đó a, b, c, d là các chữ số khác nhau từng đôi một lấy từ các chữ số đã cho, a ≠ 0.

Vì bốn chữ số được lấy từ các 6 chữ số 0; 1; 2; 3; 4; 5. Do trong dãy số này có chứa số 0 nên việc lập số có bốn chữ số cần tìm được chia thành 4 giai đoạn:

- Vì a ≠ 0 nên a có 5 cách chọn.

- b có 5 cách chọn.

- c có 4 cách chọn.

- d có 3 cách chọn.

Theo quy tắc nhân ta có: 5.5.4.3 = 300 (số).

Vậy có tất cả 300 số được lập từ các số đã cho.

Bài 3 trang 32 Toán lớp 10 Tập 2: Tổ Một có 4 bạn nam và 5 bạn nữ. Có bao nhiêu cách cử 3 bạn của tổ làm trực nhật trong mỗi trường hợp sau?

a) 3 bạn được chọn bất kì;

b) 3 bạn gồm 2 nam và 1 nữ.

Lời giải:

a) Việc chọn 3 bạn bất kì từ tổ có 9 bạn là tổ hợp chập 3 của 9. Do đó số cách chọn 3 bạn bất kì trong tổ Một là: $C_9^3=84$ (cách).

Vậy có 84 cách chọn 3 bạn của tổ làm trực nhật.

b) Việc chọn 3 bạn gồm 2 nam và 1 nữ được chia làm hai giai đoạn:

- Giai đoạn 1: Chọn 2 bạn nam từ 4 bạn nam của tổ là tổ hợp chập 2 của 4. Do đó có $C_4^2=6$(cách).

- Giai đoạn 2: Chọn 1 bạn nữ từ 5 bạn nữ của tổ là tổ hợp chập 1 của 5. Do đó có $C_5^1=5$(cách).

Theo quy tắc nhân ta có: 6.5 = 30 cách chọn tổ làm trực nhật có 3 bạn gồm 2 nam và 1 nữ.

Vậy có 30 cách cử 3 bạn của tổ làm trực nhật gồm 2 nam và 1 nữ.

Bài 4 trang 32 Toán lớp 10 Tập 2: Từ một danh sách gồm 8 người, người ta bầu ra một ủy ban gồm một chủ tịch, một phó chủ tịch, một thư kí và một ủy viên. Có bao nhiêu khả năng có thể có về kết quả bầu ủy ban này?

Lời giải:

Việc bầu ra một ủy ban gồm một chủ tịch, một phó chủ tịch, một thư kí và một ủy viên là chỉnh hợp chập 4 của 8. Do đó số khả năng có thể có về kết quả bầu ủy ban này là:

$A_8^4=1680$(cách).

Vậy có tất cả 70 khả năng có thể có về kết quả bầu ủy ban.

Bài 5 trang 32 Toán lớp 10 Tập 2: Một nhóm gồm 7 bạn đến trung tâm chăm sóc người cao tuổi làm từ thiện. Theo chỉ dẫn của trung tâm, 3 bạn hỗ trợ đi lại, 2 bạn hỗ trợ tắm rửa và 2 bạn hỗ trợ ăn uống. Có bao nhiêu cách phân công các bạn trong nhóm làm công việc trên?

Lời giải:

Công việc phân công các bạn trong nhóm làm công việc trên được chia làm ba giai đoạn:

- Giai đoạn thứ nhất: Chọn ra 3 bạn hỗ trợ đi lại từ 7 bạn là tổ hợp chập 3 của 7, do đó có $C_7^3$ cách.

- Giai đoạn thứ hai: Ứng với 3 bạn hỗ trợ đi lại, chọn 2 bạn trong 4 bạn còn lại hỗ trợ tắm rửa là tổ hợp chập 2 của 4, do đó có $C_4^2$ cách.

- Giai đoạn thứ ba: Ứng với 3 bạn hỗ trợ đi lại, 2 bạn hỗ trợ tắm rửa, chọn 2 bạn còn lại hỗ trợ ăn uống có 1 cách.

Theo quy tắc nhân, ta có: $C_7^3.C_4^2.1=210$ cách.

Vậy có tất cả 210 cách phân công các bạn trong nhóm làm công việc trên.

Bài 6 trang 32 Toán lớp 10 Tập 2: Có 4 đường thẳng song song cắt 5 đường thẳng song song khác tạo thành những hình bình hành (như Hình 10). Có bao nhiêu hình bình hành được tạo thành?

Lời giải:

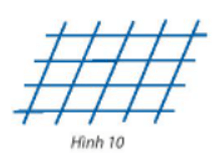
Mỗi hình bình hành được tạo bởi 2 cặp đường thẳng song song. Việc tạo hình bình hành từ 4 đường thẳng song song cắt 5 đường thẳng song song khác được chia làm hai giai đoạn:

- Giai đoạn 1: Chọn một cặp đường thẳng song song từ 4 đường thẳng song song là tổ hợp chập 4 của 2, do đó có $C_4^2$ cách.

- Giai đoạn 2: Ứng với cặp đường thẳng vừa chọn, chọn cặp đường thẳng song song từ 5 đường thẳng song song khác là tổ hợp chập 2 của 5, do đó có $C_5^2$ cách.

Theo quy tắc nhân ta có: $C_4^2.C_5^2$= 60 cách.

Vậy có tất cả 60 hình bình hành được tạo thành.

Bài 7 trang 32 Toán lớp 10 Tập 2: Mùa giải 2019, giải bóng đá vô địch quốc gia (V.League) có 14 đội bóng tham gia. Các đội bóng đấu vòng tròn hai lượt đi và lượt về. Hỏi cả giải đấu có bao nhiêu trận đấu?

Lời giải:

Cách 1:

Các đội bóng đấu vòng tròn hai lượt đi và lượt về. Khi đó việc xếp số trận đấu được chia làm 14 giai đoạn:

Đội 1 có đấu 13 trận với 13 đội còn lại;

Đội 2 có đấu 13 trận với 13 đội còn lại;

…

Đội 14 có đấu 13 trận với 13 đội còn lại.

Vậy có tất cả 13 + 13 + 13 + … + 13 (có 14 số 13) = 13.14 = 182 trận đấu.

Cách 2:

Vì việc chọn ra 2 đội bóng trong 14 đội bóng để thi đấu lượt đi và lượt về là chỉnh hợp chập 2 của 14. Do đó số trận đấu của giải bóng đá vô địch quốc gia (V.League) là: $A_{14}^2=182$ (trận).

Vậy trong cả giải đấu có tất cả 182 trận.

Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 7

Bài 1: Quy tắc cộng và quy tắc nhân

Bài 3: Nhị thức Newton

Bài tập cuối chương 8

Bài 1: Toạ độ của vectơ