Trong mặt phẳng tọa độ Oxy, cho vectơ u = (a;b). Ta chọn điểm A sao cho vectơ OA = vectơ u. Xét vectơ đơn vị i trên trục hoành Ox và vectơ đơn vị j trên trục tung Oy

Hoạt động 4 trang 63 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho vectơ $\overrightarrow{u}=\left(a;b\right)$. Ta chọn điểm A sao cho $\overrightarrow{OA}=\overrightarrow{u}$.

Xét vectơ đơn vị $\overrightarrow{i}$ trên trục hoành Ox và vectơ đơn vị $\overrightarrow{j}$ trên trục tung Oy (Hình 12).

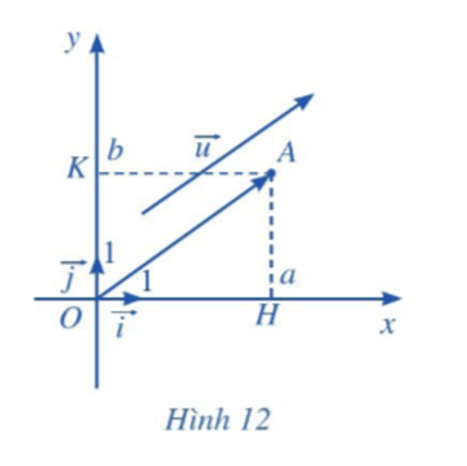
a) Tìm hoành độ và tung độ của điểm A.

b) Biểu diễn vectơ $\overrightarrow{OH}$ qua vectơ $\overrightarrow{i}$.

c) Biểu diễn vectơ $\overrightarrow{OK}$ qua vectơ $\overrightarrow{j}$.

d) Chứng tỏ rằng $\overrightarrow{u}=a\overrightarrow{i}+b\overrightarrow{j}$.

Trả lời

a) Ta có: $\overrightarrow{OA}=\overrightarrow{u}$, mà (a; b) là tọa độ của vectơ $\overrightarrow{u}$ nên điểm A có hoành độ là a và tung độ là b.

b) Điểm H biểu diễn số a trên trục Ox nên $\overrightarrow{OH}=a\overrightarrow{i}$.

c) Điểm K biểu diễn số b trên trục Oy nên $\overrightarrow{OK}=b\overrightarrow{j}$.

d) Áp dụng quy tắc hình bình hành ta có: $\overrightarrow{OA}=\overrightarrow{OK}+\overrightarrow{OH}$.

Mà $\overrightarrow{OH}=a\overrightarrow{i}$,$\overrightarrow{OK}=b\overrightarrow{j}$ nên $\overrightarrow{OA}=a\overrightarrow{i}+b\overrightarrow{j}$.

Theo bài ra ta có: $\overrightarrow{OA}=\overrightarrow{u}$.

Vậy $\overrightarrow{u}=a\overrightarrow{i}+b\overrightarrow{j}$.

Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài tập cuối chương 6

Chủ đề 2: Xây dựng mô hình hàm số bậc nhất, bậc hai biểu diễn số liệu dạng bảng

Bài 1: Tọa độ của vectơ

Bài 2: Biểu thức tọa độ của các phép toán vectơ

Bài 3: Phương trình đường thẳng

Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng