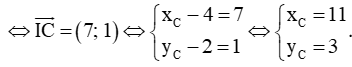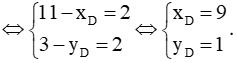Trong mặt phẳng toạ độ Oxy, cho ba điểm không thẳng hàng A(– 3; 1), B(– 1; 3), I(4; 2). Tìm toạ độ của hai điểm C, D sao cho tứ giác ABCD là hình bình hành

Bài 6 trang 66 Toán lớp 10 Tập 2: Trong mặt phẳng toạ độ Oxy, cho ba điểm không thẳng hàng A(– 3; 1), B(– 1; 3), I(4; 2). Tìm toạ độ của hai điểm C, D sao cho tứ giác ABCD là hình bình hành nhận I làm tâm đối xứng.

Trả lời

Gọi tọa độ điểm C(x_C; y_C), tọa độ điểm D(x_D; y_D).

Khi đó ta có: $\overrightarrow{AI}=\left(4-\left(-3\right);2-1\right)=\left(7;1\right)$, $\overrightarrow{IC}=\left(x_C-4;y_C-2\right)$.

Vì I là tâm đối xứng của hình bình hành ABCD nên I là trung điểm của AC, do đó

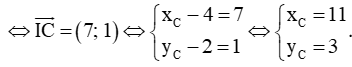
Vậy tọa độ điểm C là C(11; 3).

Ta có: $\overrightarrow{AB}=\left(\left(-1\right)-\left(-3\right);3-1\right)=\left(2;2\right)$, $\overrightarrow{DC}=\left(11-x_D;3-y_D\right)$.

Vì ABCD là hình bình hành nên $\overrightarrow{AB}=\overrightarrow{DC}$$\iff \overrightarrow{DC}=\left(2;2\right)$

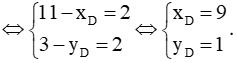
Vậy tọa độ điểm D là D(9; 1).

Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài tập cuối chương 6

Chủ đề 2: Xây dựng mô hình hàm số bậc nhất, bậc hai biểu diễn số liệu dạng bảng

Bài 1: Tọa độ của vectơ

Bài 2: Biểu thức tọa độ của các phép toán vectơ

Bài 3: Phương trình đường thẳng

Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng