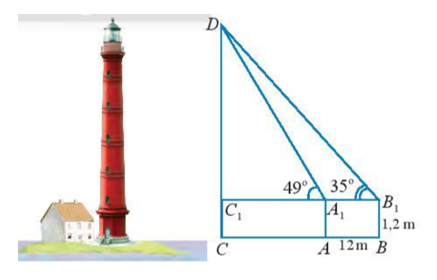
Muốn đo chiều cao của một ngọn tháp, người ta lấy hai điểm A, B trên mặt đất có khoảng cách AB = 12 m cùng thẳng hàng với chân C của tháp

Bài 10 trang 79 Toán lớp 10 Tập 1: Muốn đo chiều cao của một ngọn tháp, người ta lấy hai điểm A, B trên mặt đất có khoảng cách AB = 12 m cùng thẳng hàng với chân C của tháp để đặt hai giác kế. Chân của hai giác kế có chiều cao là h = 1,2 m. Gọi D là đỉnh tháp và hai điểm A₁, B₁ cùng thẳng hàng với C₁ thuộc chiều cao CD của tháp. Người ta đo được $\widehat{D{A}_1{C}_1}={49}^o,\widehat{D{B}_1{C}_1}={35}^o$. Tính chiều cao CD của tháp.

Trả lời

Ta có: $\widehat{D{A}_1{B}_1}={180}^0-{49}^0={131}^0$

Xét tam giác $A_1{B}_{1}D$có: $\widehat{A_{1}D{B}_1}={180}^0-(\widehat{D{A}_1{B}_1}+\widehat{A_1{B}_{1}D})={14}^0$

Áp dụng định lí sin ta có:

$\frac{A_{1}D}{\sin \widehat{D{B}_1{C}_1}}=\frac{A_1{B}_1}{\sin \widehat{A_{1}D{B}_1}}\Rightarrow A_{1}D=\frac{A_1{B}_1.\sin \widehat{D{B}_1{C}_1}}{\sin \widehat{A_{1}D{B}_1}}=\frac{12.\sin 35°}{\sin 14°}\approx 28,45$

Xét tam giác $D{C}_1{A}_1$ vuông tại $C_1$ ta có:

$\sin {49}^0=\frac{D{C}_1}{D{A}_1}\Rightarrow D{C}_1=D{A}_1.\sin {49}^0\approx 21,47m$

Ta có: CD = 21,47 + 1,2 = 22,67 m.

Vậy chiều cao của tháp khoảng 22,67 m.

Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Định lí côsin và định lí sin

Bài 3: Giải tam giác và ứng dụng thực tế

Bài tập cuối chương 4

Bài 1: Khái niệm vectơ

Bài 2: Tổng và hiệu của hai vectơ

Bài 3: Tích của một số với một vectơ