Một xưởng sản xuất những thùng bằng nhôm hình hộp chữ nhật không nắp và có các kích
51
21/04/2024
Một xưởng sản xuất những thùng bằng nhôm hình hộp chữ nhật không nắp và có các kích thước . Biết tỉ số hai cạnh đáy là , thể tích khối hộp bằng Để tốn ít vật liệu nhất thì tổng bằng:
B.
C.
D.
Trả lời
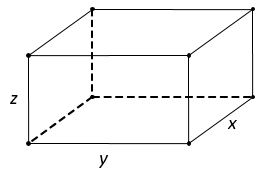
Ta có
Theo giả thiết, ta có
Tổng diện tích vật liệu (nhôm) cần dùng là: (do hộp không nắp)
Xét hàm trên , ta được nhỏ nhất khi
Khi Chọn A.
Cách 2. BĐT Côsi
Dấu xảy ra

