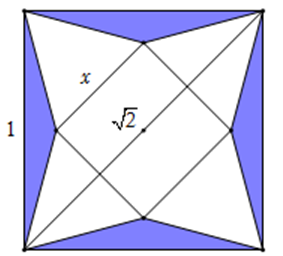
Người ta cắt một tờ giấy hình vuông cạnh bằng 1 để gấp thành một hình chóp tứ
83
21/04/2024
Người ta cắt một tờ giấy hình vuông cạnh bằng 1 để gấp thành một hình chóp tứ giác đều sao cho bốn đỉnh của hình vuông dán lại thành đỉnh của hình chóp như hình vẽ. Để thể tích khối chóp lớn nhất thì cạnh đáy x của hình chóp bằng:
A. x=√25.
B. x=2√25.
C. x=2√2.
D.x=25.
Trả lời
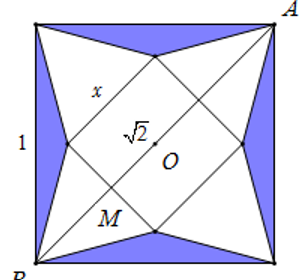
Ta có BM=BO−MO=12AB−MO=√22−x2
Chiều cao của hình chóp: h=√BM2−MO2=√(√22−x2)2−(x2)2 =√1−x√22.
Suy ra thể tích của khối chóp: V=13x2√1−x√22=13√x4−x5√22.
Khảo sát hàm f(x)=x4−x5√2 trên (0;√22) , ta được f(x) lớn nhất khi x=2√25 .
Chọn B.
Cách làm trắc nghiệm. Đầu tiên ta loại đáp án C do x=2√2∉(0;√22) . Thay ba đáp án còn lại vào hàm số f(x)=x4−x5√2 . So sánh kết quả nào lớn nhất ta chọn. Nếu đề bài hỏi giá trị lớn nhất của thể tích khối chóp thì ta không làm theo cách này được.