Cho điểm M(x0; y0) nằm trên đường tròn (C) tâm I(a; b) và cho điểm M(x; y) tùy ý trong mặt phẳng Oxy. Gọi ∆ là tiếp tuyến của (C) tại M0

Hoạt động khám phá 2 trang 61 Toán lớp 10 Tập 2: Cho điểm M(x₀; y₀) nằm trên đường tròn (C) tâm I(a; b) và cho điểm M(x; y) tùy ý trong mặt phẳng Oxy. Gọi ∆ là tiếp tuyến của (C) tại M₀.

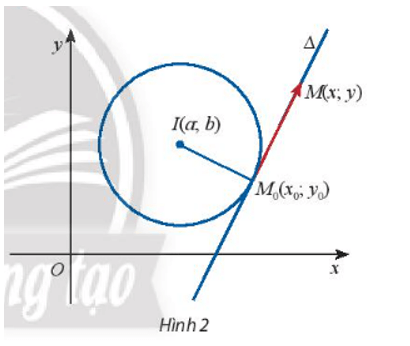
a) Viết tọa độ của hai vectơ $\overrightarrow{M_{0}M}$ và $\overrightarrow{M_{0}I}$.

b) Viết biểu thức tọa độ của tích vô hướng của hai vectơ $\overrightarrow{M_{0}M}$ và $\overrightarrow{M_{0}I}$.

c) Hệ thức $\overrightarrow{M_{0}M}.\overrightarrow{M_{0}I}=0$ cho ta phương trình của đường thẳng nào?

Trả lời

a) Biểu thức tọa độ của hai vectơ $\overrightarrow{M_{0}M}$ và $\overrightarrow{M_{0}I}$ là:

$\overrightarrow{M_{0}M}$ = (x – x₀; y – y₀);

$\overrightarrow{M_{0}I}$ = (a – x₀; b – y₀).

b) Biểu thức tọa độ tích vô hướng của hai vectơ $\overrightarrow{M_{0}M}$ và $\overrightarrow{M_{0}I}$ là:

$\overrightarrow{M_{0}M}.\overrightarrow{M_{0}I}$ = (x – x₀)(a – x₀) + (y – y₀).(b – y₀).

c) Ta có hệ thức $\overrightarrow{M_{0}M}.\overrightarrow{M_{0}I}=0$

⇔ (x – x₀)(a – x₀) + (y – y₀).(b – y₀) = 0 (*)

Vì ∆ là tiếp tuyến của đường tròn (C) nên ∆ ⊥ IM₀. Do đó phương trình đường thẳng ∆ nhận vectơ $\overrightarrow{M_{0}M}$ làm VTPT và đi qua điểm M₀(x₀; y₀) là:

(a – x₀)(x – x₀) + (b – y₀)(y – y₀) = 0

Và đây cũng chính là phương trình (*).

Vậy hệ thức $\overrightarrow{M_{0}M}.\overrightarrow{M_{0}I}=0$ là phương trình của đường thẳng ∆ là tiếp tuyến của đường tròn (C).

Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Toạ độ của vectơ

Bài 2: Đường thẳng trong mặt phẳng toạ độ

Bài 3: Đường tròn trong mặt phẳng toạ độ

Bài 4: Ba đường conic trong mặt phẳng tọa độ

Bài tập cuối chương 9

Bài 1: Không gian mẫu và biến cố