Một vận động viên ném đĩa đã vung đĩa theo một đường tròn (C) có phương trình

Vận dụng 3 trang 62 Toán lớp 10 Tập 2: Một vận động viên ném đĩa đã vung đĩa theo một đường tròn (C) có phương trình:

(x – 1)² + (y – 1)² = $\frac{169}{144}$

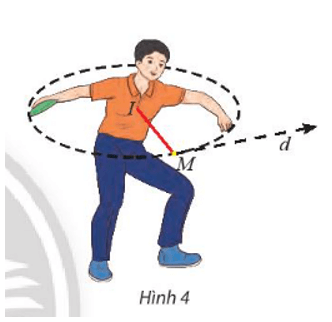
Khi người đó vung đĩa đến vị trí điểm M$\left(\frac{17}{12};2\right)$ thì buông đĩa (Hình 4). Viết phương trình tiếp tuyến của đường tròn (C) tại điểm M.

Trả lời

Phương trình đường tròn (C) có tâm I(1; 1).

Khi đó $\overrightarrow{IM}\left(\frac{5}{12};1\right)$

Phương trình tiếp tuyến của đường tròn (C) tại điểm M nhận $\overrightarrow{IM}\left(\frac{5}{12};1\right)$ làm VTPT là:

$\frac{5}{12}\left(x-\frac{17}{12}\right)+y-2=0$

⇔ $5x+12y-\frac{373}{12}=0$

Vậy phương trình tiếp tuyến của đường tròn (C) tại điểm M là $5x+12y-\frac{373}{12}=0$.

Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Toạ độ của vectơ

Bài 2: Đường thẳng trong mặt phẳng toạ độ

Bài 3: Đường tròn trong mặt phẳng toạ độ

Bài 4: Ba đường conic trong mặt phẳng tọa độ

Bài tập cuối chương 9

Bài 1: Không gian mẫu và biến cố