Lập phương trình đường tròn (C) trong các trường hợp sau: (C) có tâm I(1; 5) có bán kính r = 4

Bài 2 trang 62 Toán lớp 10 Tập 2: Lập phương trình đường tròn (C) trong các trường hợp sau:

a) (C) có tâm I(1; 5) có bán kính r = 4;

b) (C) có đường kính MN với M(3; -1) và N(9; 3);

c) (C) có tâm I(2; 1) và tiếp xúc với đường thẳng 5x – 12y + 11 = 0;

d) (C) có tâm A(1; -2) và đi qua điểm B(4; -5).

Trả lời

a) Phương trình đường tròn (C) có tâm I(1; 5) và bán kính r = 4 là:

(x – 1)² + (y – 5)² = 4²

⇔ (x – 1)² + (y – 5)² = 16.

Vậy phương trình đường tròn (C) có tâm I(1; 5) và bán kính r = 4 là (x – 1)² + (y – 5)² = 16.

b) Tâm I của đường tròn (C) là trung điểm của đoạn thẳng MN.

Khi đó tọa độ tâm I của đường tròn (C) là: I = $\left(\frac{9+3}{2};\frac{-1+3}{2}\right)=$(6; 1).

Ta có: $\overrightarrow{MN}$ = (6; 4) ⇒ MN = $\sqrt{6^2+4^2}=\sqrt{52}$

Vì MN là đường kính của đường tròn (C) nên bán kính của (C) bằng $\frac{MN}{2}=\frac{\sqrt{52}}{2}$.

Phương trình đường tròn (C) có tâm I(6; 1) và bán kính R = $\frac{\sqrt{52}}{2}$ là:

(x – 6)² + (y – 1)² = ${\left(\frac{\sqrt{52}}{2}\right)}^2$

⇔ (x – 6)² + (y – 1)² = 13.

Vậy phương trình đường tròn (C) cần tìm là (x – 6)² + (y – 1)² = 13.

c) Bán kính của đường tròn (C) là khoảng cách từ điểm I đến đường thẳng 5x – 12y + 11 = 0 là: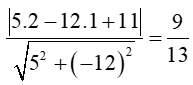 

Phương trình đường tròn (C) có tâm I(2; 1) và bán kính là R = $\frac{9}{13}$ là:

(x – 2)² + (y – 1)² = ${\left(\frac{9}{13}\right)}^2$

⇔ (x – 2)² + (y – 1)² = $\frac{81}{169}$

Vậy phương trình đường tròn (C) là (x – 2)² + (y – 1)² = $\frac{81}{169}$.

d) Bán kính của đường tròn (C) chính là độ dài đoạn thẳng AB.

Ta có $\overrightarrow{AB}$ = (3; -3) ⇒ AB = $\sqrt{3^2+{\left(-3\right)}^2}=3\sqrt{2}$.

Khi đó R = AB = 3$\sqrt{2}$

Phương trình đường tròn tâm A(1; -2) bán kính R = 3$\sqrt{2}$ là:

(x – 1)² + (y + 2)² = ${\left(3\sqrt{2}\right)}^2$

⇔ (x – 1)² + (y + 2)² = 18.

Vậy phương trình đường tròn cần tìm là (C): (x – 1)² + (y + 2)² = 18.

Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Toạ độ của vectơ

Bài 2: Đường thẳng trong mặt phẳng toạ độ

Bài 3: Đường tròn trong mặt phẳng toạ độ

Bài 4: Ba đường conic trong mặt phẳng tọa độ

Bài tập cuối chương 9

Bài 1: Không gian mẫu và biến cố