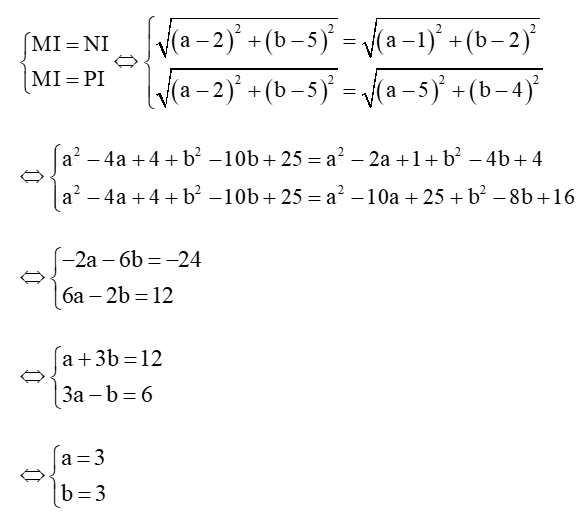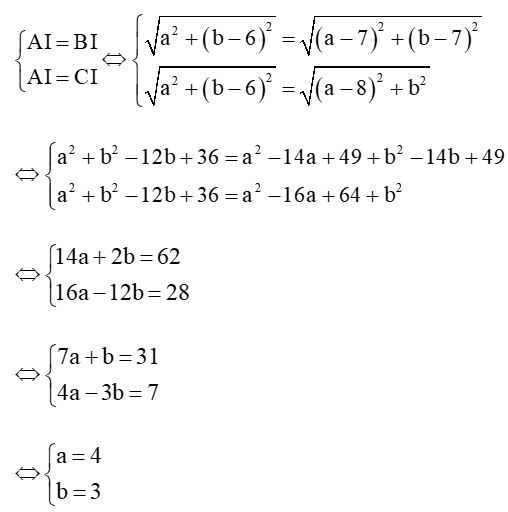Lập phương trình đường tròn ngoại tiếp tam giác có tọa độ các đỉnh là: M(2; 5), N(1; 2), P(5; 4)
1.1k
13/06/2023
Bài 3 trang 62 Toán lớp 10 Tập 2: Lập phương trình đường tròn ngoại tiếp tam giác có tọa độ các đỉnh là:
a) M(2; 5), N(1; 2), P(5; 4);
b) A(0; 6), B(7; 7), C(8; 0).
Trả lời
a) Gọi (C) là đường tròn ngoại tiếp tam giác MN P, có tâm là I(a; b) và bán kính R.
Khi đó:
→MI = (a – 2; b – 5) ⇒ MI = √(a−2)2+(b−5)2
→NI = (a – 1; b – 2) ⇒ NI = √(a−1)2+(b−2)2
→PI = (a – 5; b – 4) ⇒ PI = √(a−5)2+(b−4)2
Ta có: MI = NI = PI = R nên ta có hệ phương trình:
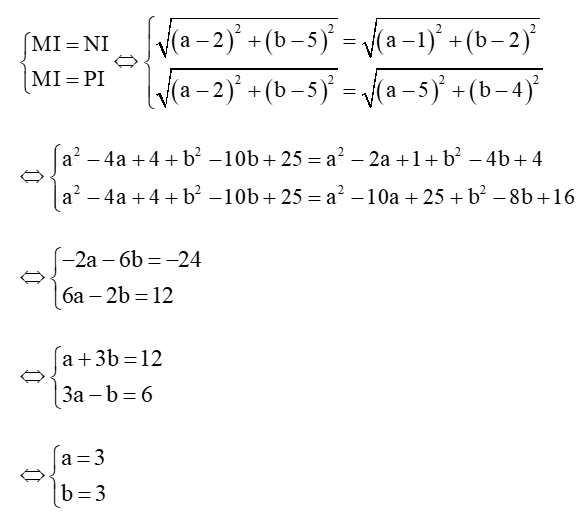
⇒ I(3; 3) và MI = √(3−2)2+(3−5)2=√5.
Do đó phương trình đường tròn ngoại tiếp tam giác MNP có tâm I(3; 3) và bán kính R = √5 là:
(x – 3)2 + (y – 3)2 = (√5)2
⇔ (x – 3)2 + (y – 3)2 = 5.
Vậy phương trình đường tròn ngoại tiếp tam giác MNP là: (x – 3)2 + (y – 3)2 = 5.
b) Gọi (C) là đường tròn ngoại tiếp tam giác ABC, có tâm là I(a; b) và bán kính R.
Khi đó:
→AI = (a ; b – 6) ⇒ AI = √a2+(b−6)2
→BI = (a – 7; b – 7) ⇒ BI = √(a−7)2+(b−7)2
→CI = (a – 8; b) ⇒ CI = √(a−8)2+b2
Ta có: AI = BI = CI = R nên ta có hệ phương trình:
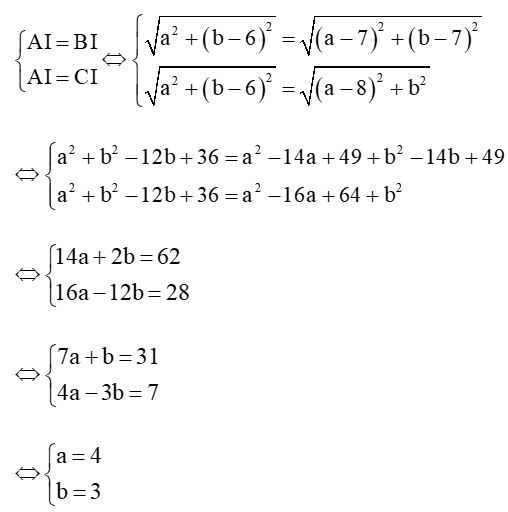
⇒ I(4; 3) và AI = √42+(3−6)2=√25=5.
Do đó phương trình đường tròn ngoại tiếp tam giác ABC có tâm I(4; 3) và bán kính R = 5 là:
(x – 4)2 + (y – 3)2 = 52
⇔ (x – 4)2 + (y – 3)2 = 25.
Vậy phương trình đường tròn ngoại tiếp tam giác ABC là: (x – 4)2 + (y – 3)2 = 25.
Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Toạ độ của vectơ
Bài 2: Đường thẳng trong mặt phẳng toạ độ
Bài 3: Đường tròn trong mặt phẳng toạ độ
Bài 4: Ba đường conic trong mặt phẳng tọa độ
Bài tập cuối chương 9
Bài 1: Không gian mẫu và biến cố