Hình 46 mô phỏng một trạm thu phát sóng điện thoại di động đặt ở vị trí I có toạ độ (– 2; 1) trong mặt phẳng toạ độ (đơn vị trên hai trục là ki-lô-mét)

Bài 6 trang 92 Toán 10 Tập 2: Hình 46 mô phỏng một trạm thu phát sóng điện thoại di động đặt ở vị trí I có toạ độ (– 2; 1) trong mặt phẳng toạ độ (đơn vị trên hai trục là ki-lô-mét).

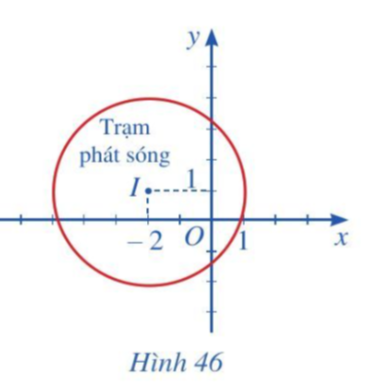
a) Lập phương trình đường tròn mô tả ranh giới bên ngoài của vùng phủ sóng, biết rằng trạm thu phát sóng đó được thiết kế với bán kính phủ sóng 3 km.

b) Nếu người dùng điện thoại ở vị trí có toạ độ (– 1; 3) thì có thể sử dụng dịch vụ của trạm này không? Giải thích.

c) Tính theo đường chim bay, xác định khoảng cách ngắn nhất để một người ở vị trí có toạ độ (– 3; 4) di chuyển được tới vùng phủ sóng theo đơn vị ki-lô-mét (làm tròn kết quả đến hàng phần mười).

Trả lời

a) Đường tròn mô tả ranh giới bên ngoài của vùng phủ sóng có tâm I(– 2; 1) và bán kính R = 3.

Vậy phương trình đường tròn là

[x – (– 2)]² + (y – 1)² = 3² hay (x + 2)² + (y – 1)² = 9.

b) Gọi M(– 1; 3) là vị trí của người dùng điện thoại.

Khoảng cách từ tâm I của đường tròn mô tả ranh giới bên ngoài của vùng phủ sóng tới vị trí M(– 1; 3) là

IM = $\sqrt{{\left(\left(-1\right)-\left(-2\right)\right)}^2+{\left(3-1\right)}^2}=\sqrt{5}$.

Mà $\sqrt{5}<3$ nên IM < R.

Khi đó vị trí M(– 1; 3) nằm trong đường tròn mô tả ranh giới bên ngoài của vùng phủ sóng.

Vậy người dùng điện thoại ở vị trí có tọa độ (– 1; 3) có thể sử dụng dịch vụ của trạm thu  phát sóng này.

c) Gọi vị trí người đó đang đứng là A(– 3; 4).

Ta có: $\overrightarrow{AI}=\left(-2-\left(-3\right);1-4\right)$, do đó $\overrightarrow{AI}=\left(1;-3\right)$.

Suy ra $AI=\sqrt{1^2+{\left(-3\right)}^2}=\sqrt{10}$ > 3 = R.

Vì AI > R nên A nằm ngoài đường tròn ranh giới.

Giả sử đường thẳng AI cắt đường tròn tại điểm B.

Do đó, AB là khoảng cách từ A đến vùng phủ sóng.

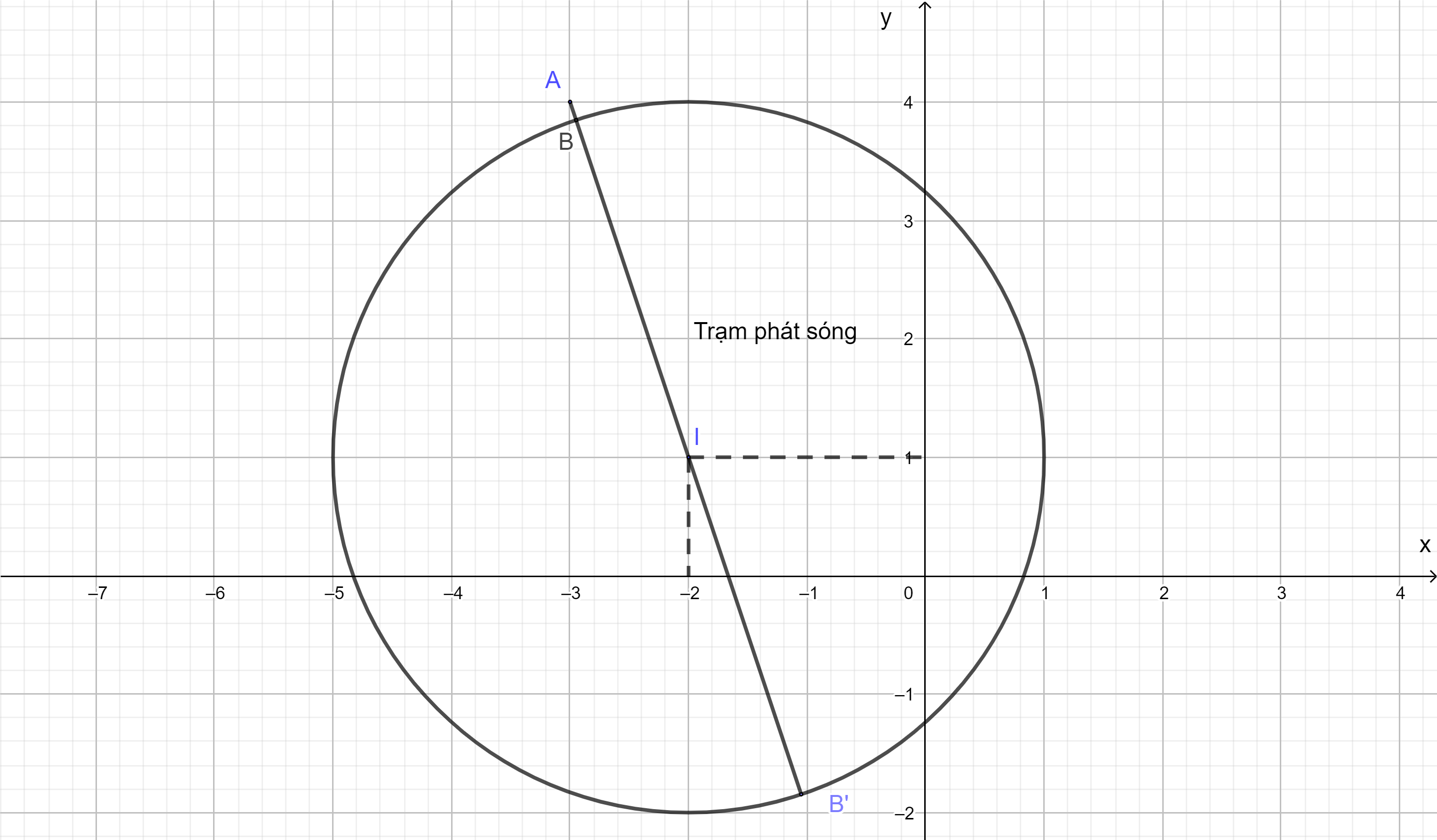
Đường thẳng AI có vectơ $\overrightarrow{AI}=\left(1;-3\right)$ vectơ chỉ phương.

Suy ra AI có vectơ pháp tuyến là $\overrightarrow{n}=\left(3;1\right)$.

Vậy phương trình đường thẳng AI là

3(x + 3) + 1(y – 4) = 0 hay 3x + y + 5 = 0.

Vì B là giao điểm của AI và đường tròn mô tả ranh giới nên tọa độ của điểm B là nghiệm của hệ phương trình $\left\{\begin{array}{l}3x+y+5=0\\ {\left(x+2\right)}^2+{\left(y–1\right)}^2=9\end{array}\right.$.

Giải hệ phương trình ta có:

$\left\{\begin{array}{l}3x+y+5=0\\ {\left(x+2\right)}^2+{\left(y–1\right)}^2=9\end{array}\right.$

$\iff \left\{\begin{array}{l}y=-3x-5\\ {\left(x+2\right)}^2+{\left(-3x-5-1\right)}^2=9\end{array}\right.$

$\iff \left\{\begin{array}{l}y=-3x-5\\ x^2+4x+4+9x^2+36x+36=9\end{array}\right.$ 

$\iff \left\{\begin{array}{l}y=-3x-5\\ 10x^2+40x+31=0\end{array}\right.$

$\iff \left\{\begin{array}{l}y=-3x-5\\ \left[\begin{array}{l}x=\frac{-20+3\sqrt{10}}{10}\\ x=\frac{-20-3\sqrt{10}}{10}\end{array}\right.\end{array}\right.$

$\iff \left[\begin{array}{l}\left\{\begin{array}{l}x=\frac{-20+3\sqrt{10}}{10}\\ y=\frac{10-9\sqrt{10}}{10}\end{array}\right.\\ \left\{\begin{array}{l}x=\frac{-20-3\sqrt{10}}{10}\\ y=\frac{10+9\sqrt{10}}{10}\end{array}\right.\end{array}\right.\iff \left[\begin{array}{l}B\left(\frac{-20+3\sqrt{10}}{10};\frac{10-9\sqrt{10}}{10}\right)\\ B\left(\frac{-20-3\sqrt{10}}{10};\frac{10+9\sqrt{10}}{10}\right)\end{array}\right.$

+ Với $B\left(\frac{-20+3\sqrt{10}}{10};\frac{10-9\sqrt{10}}{10}\right)$

Ta có: $AB=\sqrt{{\left(\frac{-20+3\sqrt{10}}{10}-\left(-3\right)\right)}^2+{\left(\frac{10-9\sqrt{10}}{10}-4\right)}^2}\approx \mathrm{6,2}$

+ Với $B\left(\frac{-20-3\sqrt{10}}{10};\frac{10+9\sqrt{10}}{10}\right)$

Ta có: $AB=\sqrt{{\left(\frac{-20-3\sqrt{10}}{10}-\left(-3\right)\right)}^2+{\left(\frac{10+9\sqrt{10}}{10}-4\right)}^2}\approx \mathrm{0,2}$

Vì 0,2 < 6,2 mà khoảng cách cần xác định là ngắn nhất nên AB ≈ 0,2.

Vậy tính theo đường chim bay, khoảng cách ngắn nhất để một người ở vị trí có toạ độ (– 3; 4) di chuyển được tới vùng phủ sóng khoảng 0,2 km.

Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 3: Phương trình đường thẳng

Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng

Bài 5: Phương trình đường tròn

Bài 6: Ba đường conic

Bài tập cuối chương 7

Thực hành phần mềm Geogebra