Cho điểm M0(x0; y0) nằm trên đường tròn (C) tâm I(a; b) bán kính R. Gọi ∆ là tiếp tuyến tại điểm M0(x0; y0) thuộc đường tròn (Hình 44)

Hoạt động 4 trang 90 Toán 10 Tập 2: Cho điểm M₀(x₀; y₀) nằm trên đường tròn (C) tâm I(a; b) bán kính R.

Gọi ∆ là tiếp tuyến tại điểm M₀(x₀; y₀) thuộc đường tròn (Hình 44).

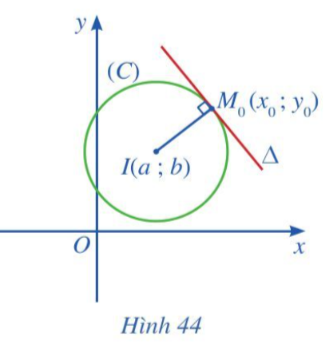
a) Chứng tỏ rằng $\overrightarrow{I{M}_0}$ là vectơ pháp tuyến của đường thẳng ∆.

b) Tính tọa độ của $\overrightarrow{I{M}_0}$.

c) Lập phương trình tổng quát của đường thẳng ∆.

Trả lời

a) Đường thẳng ∆ là tiếp tuyến của đường tròn (C) có tâm I tại điểm M₀ nên IM₀ vuông góc với ∆ tại M₀ (định nghĩa tiếp tuyến).

Vậy vectơ $\overrightarrow{I{M}_0}$ là vectơ pháp tuyến của đường thẳng ∆.

b) Ta có: $\overrightarrow{I{M}_0}=\left(x_0-a;y_0-b\right)$.

c) Đường thẳng ∆ đi qua điểm M₀(x₀; y₀) và có $\overrightarrow{I{M}_0}$ là vectơ pháp tuyến.

Vậy phương trình tổng quát của đường thẳng ∆ là(x₀ – a)(x – x₀) + (y₀ – b)(y – y₀) = 0.

Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 3: Phương trình đường thẳng

Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng

Bài 5: Phương trình đường tròn

Bài 6: Ba đường conic

Bài tập cuối chương 7

Thực hành phần mềm Geogebra