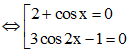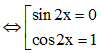Giải các phương trình sau: a) (2 + cos x)(3cos 2x – 1) = 0; b) 2sin 2x – sin 4x = 0

Bài 1.27 trang 24 SBT Toán 11 Tập 1: Giải các phương trình sau:

a) (2 + cos x)(3cos 2x – 1) = 0;

b) 2sin 2x – sin 4x = 0;

c) cos⁶ x – sin⁶ x = 0;

d) tan 2x cot x = 1. 

Trả lời

a) Ta có (2 + cos x)(3cos 2x – 1) = 0

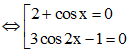
+ Phương trình 2 + cos x = 0 vô nghiệm vì – 1 ≤ cos x ≤ 1.

+ Gọi α là góc thoả mãn cos α = $\frac{1}{3}$ . Ta có

3cos 2x – 1 = 0 ⇔ cos 2x = cos α ⇔ 2x = ± α + k2π (k ∈ ℤ) ⇔ x = $\pm \frac{\alpha }{2}$  + kπ (k ∈ ℤ).

Vậy nghiệm của phương trình đã cho là x = $\pm \frac{\alpha }{2}$  + kπ (k ∈ ℤ) với cos α = $\frac{1}{3}$ .

b) Ta có 2sin 2x – sin 4x = 0

⇔ 2sin 2x – 2sin 2x cos 2x = 0

⇔ 2sin 2x(1 – cos2x) = 0

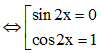
Do sin² 2x + cos² 2x = 1 nên cos 2x = 1 kéo theo sin 2x = 0, do đó phương trình đã cho tương đương với

sin 2x = 0 ⇔ 2x = kπ (k ∈ ℤ) $\iff x=k\frac{\pi }{2}\left(k\in \mathbb{Z}\right)$ .

c) Ta có cos⁶ x – sin⁶ x = 0

⇔ cos⁶ x = sin⁶ x

⇔ (cos² x)³ = (sin² x)³

⇔ cos² x = sin² x

⇔ cos² x – sin² x = 0

⇔ cos 2x = 0

Từ đó ta được 2x = $\frac{\pi }{2}$  + kπ (k ∈ ℤ) hay $x=\frac{\pi }{4}+k\frac{\pi }{2}\left(k\in \mathbb{Z}\right)$ .

d) Điều kiện sin x ≠ 0 và cos 2x ≠ 0.

Ta có tan 2x cot x = 1

$\iff \tan 2x=\frac{1}{\cot x}$

⇔ tan 2x = tan x

⇔ 2x = x + kπ   (k ∈ ℤ)

⇔ x = kπ   (k ∈ ℤ).

Ta thấy x = kπ (k ∈ ℤ) không thoả mãn điều kiện sin x ≠ 0.

Vậy phương trình đã cho vô nghiệm.

Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 2: Công thức lượng giác

Bài 3: Hàm số lượng giác

Bài 4: Phương trình lượng giác cơ bản

Bài tập cuối chương 1

Bài 5: Dãy số

Bài 6: Cấp số cộng