Dùng đồ thị hàm số y = sin x, y = cos x để xác định số nghiệm của phương trình: a) 5sin x – 3 = 0

Bài 61 trang 31 SBT Toán 11 Tập 1: Dùng đồ thị hàm số y = sin x, y = cos x để xác định số nghiệm của phương trình:

a) 5sin x – 3 = 0 trên đoạn [– π; 4π];

b) $\sqrt{2}$ cos x + 1 = 0 trên khoảng (– 4π; 0).

Trả lời

a) Ta có 5sin x – 3 = 0 $\iff \sin x=\frac{3}{5}$ .

Do đó, số nghiệm của phương trình 5sin x – 3 = 0 trên đoạn [– π; 4π] bằng số giao điểm của đồ thị hàm số y = sin x trên đoạn [– π; 4π] và đường thẳng $\iff \sin x=\frac{3}{5}$ .

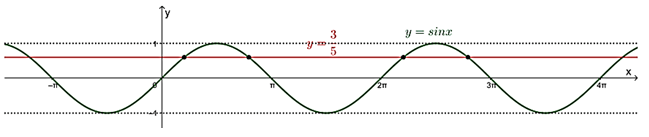
Dựa vào đồ thị, ta thấy đồ thị hàm số y = sin x trên đoạn [– π; 4π] và đường thẳng $y=\frac{3}{5}$  cắt nhau tại 4 điểm phân biệt.

Vậy phương trình 5sin x – 3 = 0 có 4 nghiệm trên đoạn [– π; 4π].

b) Ta có $\sqrt{2}$ cos x + 1 = 0 $\iff \cos x=-\frac{1}{\sqrt{2}}$ .

Do đó, số nghiệm của phương trình $\sqrt{2}$ cos x + 1 = 0 trên đoạn (– 4π; 0) bằng số giao điểm của đồ thị hàm số y = cos x trên đoạn (– 4π; 0) và đường thẳng $y=-\frac{1}{\sqrt{2}}$ .

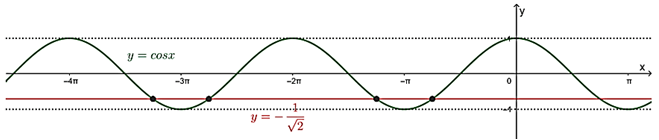
Dựa vào đồ thị, ta thấy đồ thị hàm số y = cos x trên đoạn (– 4π; 0) và đường thẳng $y=-\frac{1}{\sqrt{2}}$  cắt nhau tại 4 điểm phân biệt.

Vậy phương trình $\sqrt{2}$ cos x + 1 = 0 có 4 nghiệm trên khoảng (– 4π; 0).

Xem thêm lời giải bài tập SBT Toán 11 Cánh diều hay, chi tiết khác:

Bài 2: Các phép biến đổi lượng giác

Bài 3: Hàm số lượng giác và đồ thị

Bài 4: Phương trình lượng giác cơ bản

Bài tập cuối chương 1

Bài 1: Dãy số

Bài 2: Cấp số cộng