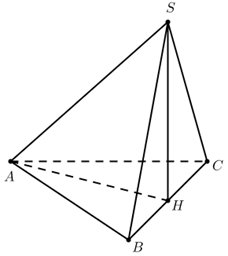
Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân tại A, BC = a căn bậc hai của 2. Hình chiếu vuông góc H của S trên mặt phẳng đáy là trung điểm của đoạn thẳng BC và SA = a căn bậc hai của
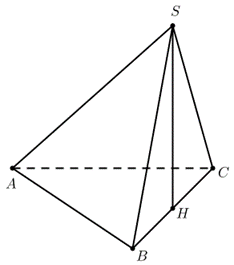
Cho khối chóp \[S.ABC{\rm{ }}\]có đáy \[ABC{\rm{ }}\]là tam giác vuông cân tại \[A\], \[BC = a\sqrt 2 \]. Hình chiếu vuông góc \[H\] của \[S\] trên mặt phẳng đáy là trung điểm của đoạn thẳng \[BC\] và \[SA = \frac{{a\sqrt 3 }}{2}\] (tham khảo hình vẽ dưới đây). Tính thể tích \[V\] của khối chóp đã cho.
A. \(V = \frac{{{a^3}}}{{12}}\).
B. \(V = \frac{{{a^3}\sqrt 3 }}{4}\).
C. \(V = \frac{{{a^3}}}{4}\).
D. \(V = \frac{{{a^3}\sqrt 3 }}{{12}}\).