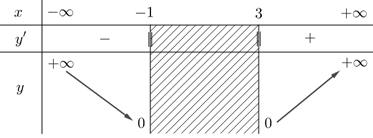
Cho hàm số y = căn bậc hai của x^2 - 2x - 3. Khẳng định nào sau đây là đúng? A. maxy = 1 B. maxy = 2 C. maxy = 0 D. Hàm số không có giá trị lớn nhất.
69
06/05/2024
Cho hàm số \(y = \sqrt {{x^2} - 2x - 3} \). Khẳng định nào sau đây là đúng?
A. \({\rm{max}}y = 1\).
B. \({\rm{max}}y = 2\).
C. \({\rm{max}}y = 0\).
D. Hàm số không có giá trị lớn nhất.
Trả lời
Lời giải
Chọn D
Điều kiện xác định: \({x^2} - 2x - 3 \ge 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x \ge 3}\\{x \le - 1}\end{array}} \right.\)
\( \Rightarrow \) Tập xác định: \(D = \left( { - \infty ; - 1} \right] \cup \left[ {3; + \infty } \right)\)
\(y{\rm{'}} = \frac{{2x - 2}}{{2\sqrt {{x^2} - 2x - 3} }} = \frac{{x - 1}}{{\sqrt {{x^2} - 2x - 3} }} = 0 \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1}\\{{x^2} - 2x - 3 > 0}\end{array}} \right. \Leftrightarrow VN\)
Bảng biến thiên:
Dựa vào bảng biến thiên, Suy ra KQ.
