Cho hàm số y = f( x ). Hàm số y = f'( x )có đồ thị như hình bên. Hàm số g( x ) = f( x^2 + 2x) - x^2 - 2x đồng biến trên khoảng nào dưới đây? A. ( - 1 - căn bậc hai của 2 ; - 1).
93
06/05/2024
Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\)có đồ thị như hình bên.
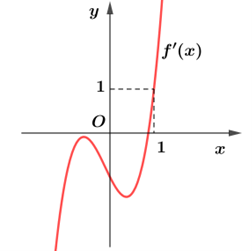
Hàm số \(g\left( x \right) = f\left( {{x^2} + 2x} \right) - {x^2} - 2x\)đồng biến trên khoảng nào dưới đây?
A. \(\left( { - 1 - \sqrt 2 ; - 1} \right)\).
B. \(\left( { - 1 - \sqrt 2 ; - 1 + \sqrt 2 } \right)\).
C. \(\left( { - 1; + \infty } \right)\).
D. \(\left( { - 1; - 1 + \sqrt 2 } \right)\).
Trả lời
Lời giải
Chọn A
Ta có: \(g\left( x \right) = f\left( {{x^2} + 2x} \right) - {x^2} - 2x\)
\( \Rightarrow g'\left( x \right) = \left( {2x + 2} \right)f'\left( {{x^2} + 2x} \right) - 2x - 2 = 2\left( {x + 1} \right)\left[ {f'\left( {{x^2} + 2x} \right) - 1} \right]\).
\( \Rightarrow g'\left( x \right) = 0 \Leftrightarrow 2\left( {x + 1} \right)\left[ {f'\left( {{x^2} + 2x} \right) - 1} \right] = 0 \Leftrightarrow x = - 1,x = - 1 + \sqrt 2 ,x = - 1 - \sqrt 2 \)
Xét\(g'\left( x \right) > 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{x + 1 > 0}\\{f'\left( {{x^2} + 2x} \right) > 1}\end{array}} \right.\left( I \right)}\\{\left\{ {\begin{array}{*{20}{c}}{x + 1 < 0}\\{f'\left( {{x^2} + 2x} \right) < 1}\end{array}} \right.\left( {II} \right)}\end{array}} \right.\).
Xét sự tương giao của đồ thị hàm số \(y = f'\left( x \right)\)và \(y = 1\).
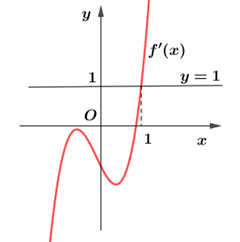
Dựa vào đồ thị ta có: \(f'\left( {{x^2} + 2x} \right) > 1 \Leftrightarrow {x^2} + 2x > 1\)và \(f'\left( {{x^2} + 2x} \right) < 1 \Leftrightarrow {x^2} + 2x < 1\).
Xét hệ (I): \(\left\{ {\begin{array}{*{20}{c}}{x + 1 > 0}\\{f'\left( {{x^2} + 2x} \right) > 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x > - 1}\\{{x^2} + 2x > 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x > - 1}\\{\left[ {\begin{array}{*{20}{c}}{x > - 1 + \sqrt 2 }\\{x < - 1 - \sqrt 2 }\end{array}} \right.}\end{array}} \right. \Leftrightarrow x > - 1 + \sqrt 2 \).
Xét hệ (II):\(\left\{ {\begin{array}{*{20}{c}}{x + 1 < 0}\\{f'\left( {{x^2} + 2x} \right) < 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x < - 1}\\{{x^2} + 2x < 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x < - 1}\\{ - 1 - \sqrt 2 < x < - 1 + \sqrt 2 }\end{array}} \right.\)
\( \Leftrightarrow - 1 - \sqrt 2 < x < - 1\).
Vậy hàm số \(g\left( x \right)\)đồng biến trên khoảng \(\left( { - 1 - \sqrt 2 ; - 1} \right)\)và \(\left( { - 1 + \sqrt 2 ; + \infty } \right)\).


