Cho hàm số y = f( x ) có bảng biến thiên như sau Số nghiệm thuộc [ 0; 3pi /2] của phương trình | f( cos 2x)| = 1 là A. 9 B. 4 C. 7 D. 10
100
06/05/2024
Cho hàm số y=f(x) có bảng biến thiên như sau
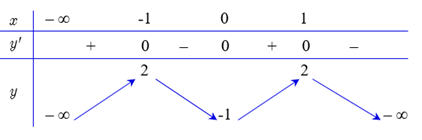
Số nghiệm thuộc [0;3π2] của phương trình |f(cos2x)|=1 là
A. 9.
B. 4.
C. 7.
D. 10.
Trả lời
Lời giải
Chọn A
Từ bảng biến thiên của f(x) ta suy ra bảng biến thiên của |f(x)| như sau
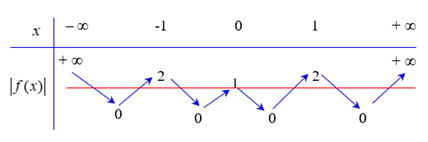
Đặt t=cos2x∈[−1;1].
Dựa vào bảng biến thiên trên, phương trình |f(t)|=1 chỉ có 3 nghiệm thuộc (−1;1).
Ta có |f(t)|=1⇔[t=a∈(−1;0)t=0t=b∈(0;1).
Do x∈[0;3π2]⇔2x∈[0;3π].
Xét đường tròn lượng giác
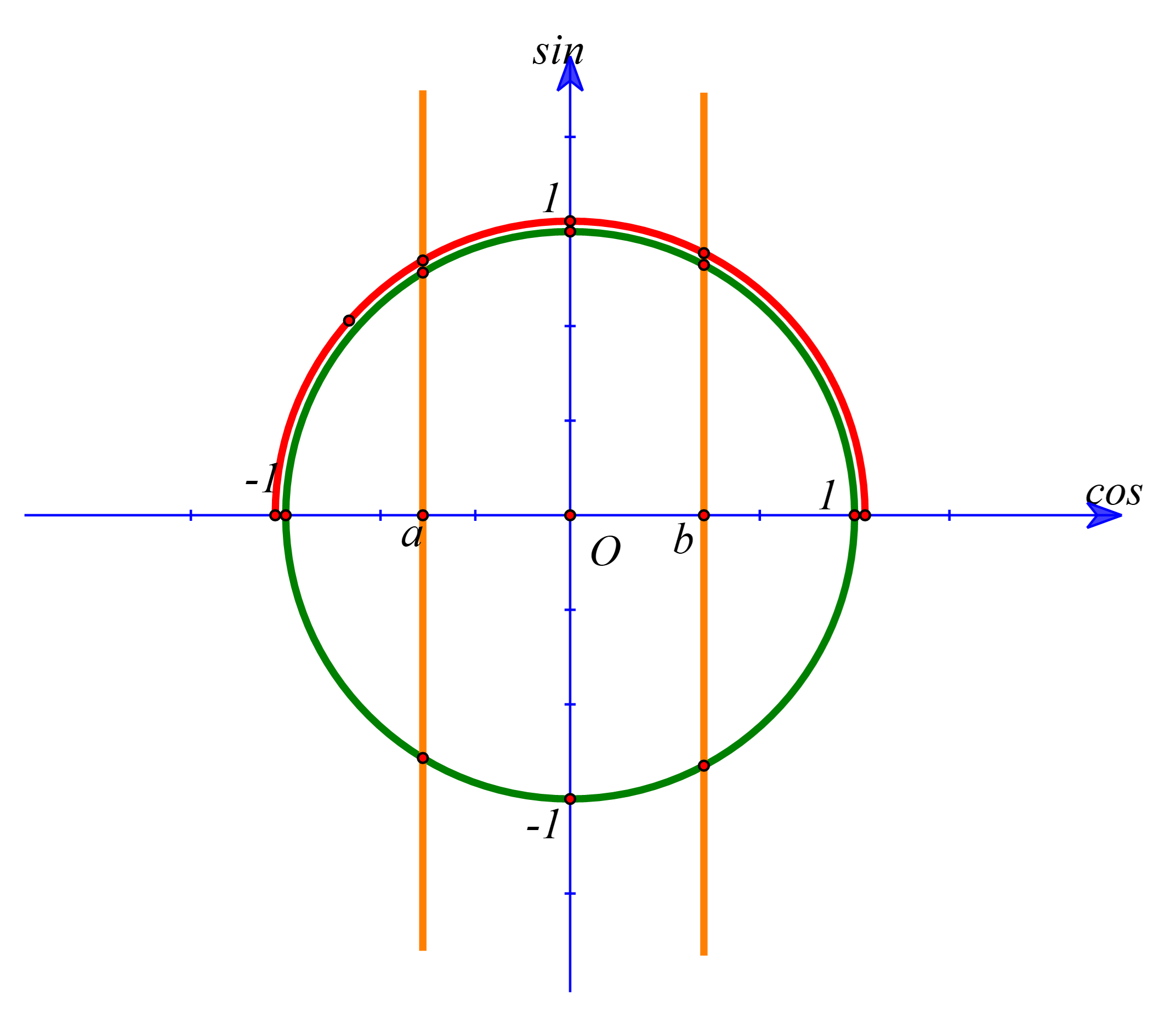
Phương trình cos2x=a,a∈(−1;0) có 3 nghiệm phân biệt thuộc [0;3π2].
Phương trình cos2x=b,a∈(0;1) có 3 nghiệm phân biệt thuộc [0;3π2].
Phương trình cos2x=0 có 3 nghiệm phân biệt thuộc [0;3π2].
Vậy số nghiệm thuộc [0;3π2] của phương trình |f(cos2x)|=1 là 9 nghiệm.
Phân tích phương án nhiễu:
B: Học sinh nhầm |f(cos2x)|=1 chỉ có 4 nghiệm phân biệt dựa vào BBT.
C: Học sinh nhầm |f(cos2x)|=1 có 7 nghiệm phân biệt dựa vào BBT sau khi lấy đối xứng.
D: Học sinh nhầm |f(cos2x)|=1 có 10 nghiệm phân biệt do nhầm lẫn sin2x và cos2x.



