Đường cong ở hình vẽ dưới đây là đồ thị của hàm số y = ax + b/cx + d với (a,b,c,d) là các số thực. Mệnh đề nào dưới đây đúng ? A. y' < 0, x khác - 1. B. y' > 0, x thuộc R C. y' > 0, x
Đường cong ở hình vẽ dưới đây là đồ thị của hàm số \(y = \frac{{ax + b}}{{cx + d}}\) với \(a,b,c,d\) là các số thực.
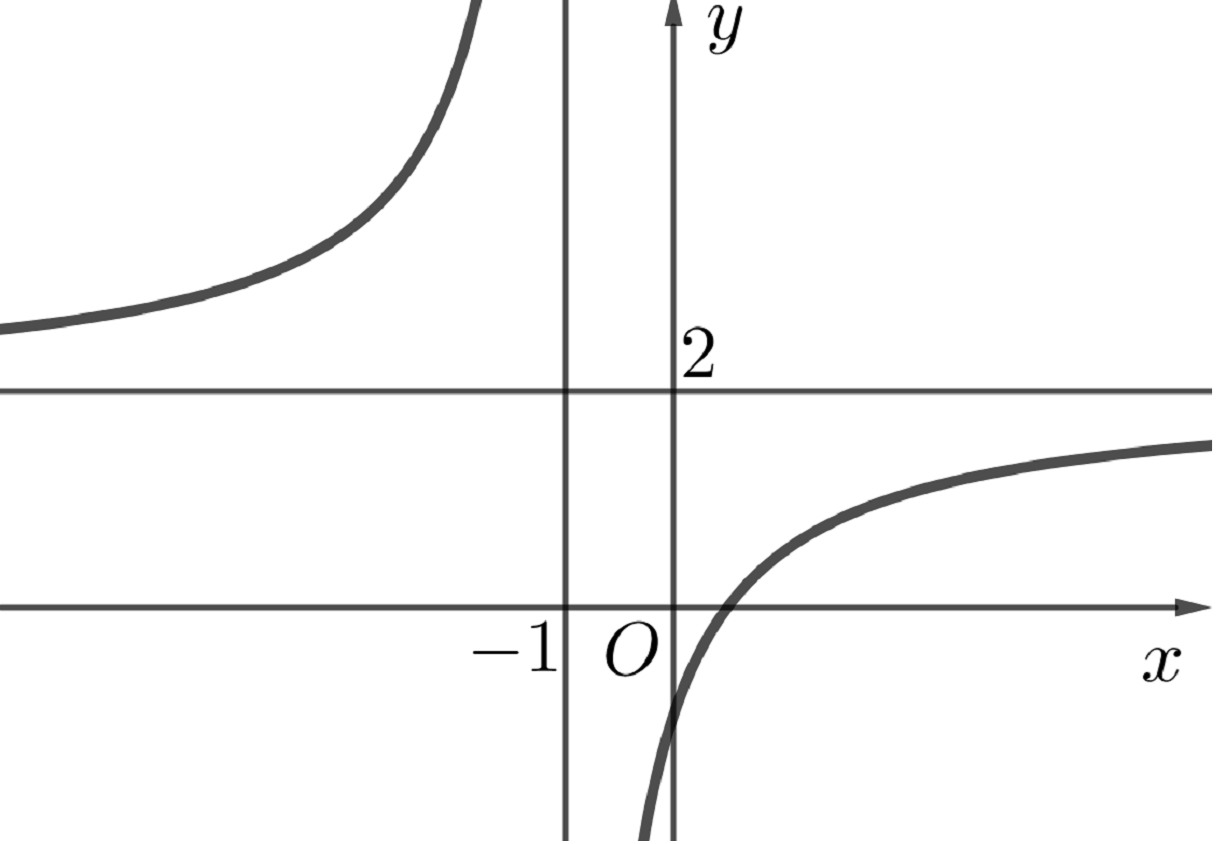
Mệnh đề nào dưới đây đúng ?
A. \(y' < 0,\forall x \ne - 1.\)
B. \(y' > 0,\forall x \in \mathbb{R}.\)
C. \(y' > 0,\forall x \ne 2.\)
D. \(y' > 0,\forall x \ne - 1.\)
