Cho hàm số y = f( x ) xác định, liên tục trên R và có đúng hai điểm cực trị x = - 1,x = 1, có đồ thị như hình vẽ sau: Hỏi hàm số y = f( x^2 - 2x + 1) + 2020 có bao nhiêu điểm cực tiểu?
101
06/05/2024
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có đúng hai điểm cực trị \(x = - 1,x = 1,\) có đồ thị như hình vẽ sau:
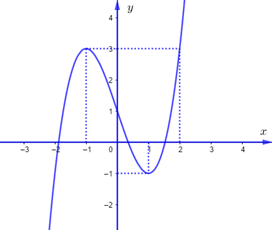
Hỏi hàm số \(y = f\left( {{x^2} - 2x + 1} \right) + 2020\) có bao nhiêu điểm cực tiểu?
A. \(4\).
B. \(3\).
C. \(2\).
D. \(1\).
Trả lời
Lời giải
Chọn C
Do hàm số \(y = f\left( x \right)\) có đúng hai điểm cực trị \(x = - 1,x = 1\)nên phương trình \(f'\left( x \right) = 0\) có hai nghiệm bội lẻ phân biệt \(x = - 1,x = 1\). Dấu của \(f'\left( x \right)\)
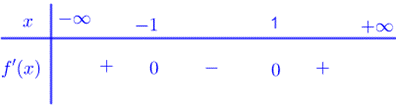
Ta có \(y' = \left( {2x - 2} \right)f'\left( {{x^2} - 2x + 1} \right)\).
\(y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x - 2 = 0}\\{{x^2} - 2x + 1 = - 1}\\{{x^2} - 2x + 1 = 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = 0}\\{x = 2}\end{array}} \right.\).
Ta có: 3 nghiệm 0, 1, 2 của \(y' = 0\) đều là nghiệm bội lẻ nên \(y'\) đổi dấu khi qua các điểm này. Mặt khác với \(x > 2\) thì \(2x - 2 > 0\) và \({x^2} - 2x + 1 > 0,f'\left( {{x^2} - 2x + 1} \right) > 0\).
Do đó ta có bảng biến thiên:
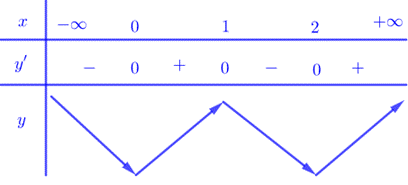
Từ bảng biến thiên ta suy ra hàm số \(y = f\left( {{x^2} - 2x + 1} \right) + 2020\) có 2 điểm cực tiểu.