Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với mặt đáy ( ABC), BC = a, góc hợp bởi (SBC) và ( ABC) là 60^0. Mặt phẳng ( P )qua A vuông góc với SC cắt SB,SC lần l
61
06/05/2024
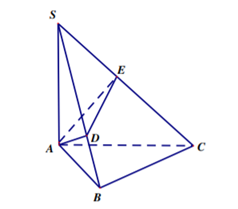
Cho hình chóp \(S.ABC\)có đáy \(ABC\)là tam giác vuông cân tại \(B\), \(SA\)vuông góc với mặt đáy\(\left( {ABC} \right),\;BC = a\), góc hợp bởi \(\left( {SBC} \right)\)và \(\left( {ABC} \right)\)là \({60^ \circ }\). Mặt phẳng \(\left( P \right)\)qua \(A\)vuông góc với \(SC\)cắt \(SB,SC\)lần lượt tại \(D,E\). Thể tích khối đa diện \(ABCED\)là
A. \(\frac{{3\sqrt 3 {a^3}}}{{40}}\).
B. \(\frac{{\sqrt 3 {a^3}}}{6}\).
C. \(\frac{{11\sqrt 3 {a^3}}}{{120}}\).
D. \(\frac{{3\sqrt 3 {a^3}}}{{60}}\).
Trả lời
Lời giải
Chọn C
Ta có \(\left\{ {\begin{array}{*{20}{c}}{BC \bot BA}\\{BC \bot SA}\end{array}} \right. \Rightarrow BC \bot \left( {SBA} \right) \Rightarrow BC \bot SB\). Do đó góc \(\angle SBA\)là góc giữa\(\left( {SBC} \right)\)và \(\left( {ABC} \right)\).
Từ đó suy ra \(\angle SBA = {60^ \circ }\). Tam giác \(SBA\)vuông có \(SA = AB\tan {60^ \circ } = a\sqrt 3 \)
Ta có \(BC \bot \left( {SAB} \right) \Rightarrow BC \bot AD;\left\{ {\begin{array}{*{20}{c}}{AD \bot BC}\\{AD \bot SC}\end{array}} \right. \Rightarrow AD \bot SB\).
\(\frac{{{V_{S.ADE}}}}{{{V_{S.ABC}}}} = \frac{{SA}}{{SA}}.\frac{{SD}}{{SB}}.\frac{{SE}}{{SC}} = \frac{{SD.SB}}{{S{B^2}}}.\frac{{SE.SC}}{{S{C^2}}} = \frac{{S{A^2}}}{{S{B^2}}}.\frac{{S{A^2}}}{{S{C^2}}} = \frac{{9{a^4}}}{{4{a^2}.5{a^2}}} = \frac{9}{{20}}\).
\({V_{S.ABC}} = \frac{1}{3}SA.{S_{ABC}} = \frac{1}{3}\sqrt 3 a.\frac{{{a^2}}}{2} = \frac{{\sqrt 3 {a^3}}}{6}\).
Vậy \({V_{ABCED}} = \frac{{11}}{{20}}.{V_{S.ABC}} = \frac{{11\sqrt 3 {a^3}}}{{120}}\).
