Cho hình chóp tứ giác đều S.ABCD với O là tâm của đáy và có tất cả các cạnh đều bằng a

Thực hành 2 trang 85 Toán 11 Tập 2: Cho hình chóp tứ giác đều S.ABCD với O là tâm của đáy và có tất cả các cạnh đều bằng a. Xác định và tính góc phẳng nhị diện:

a) [S, BC, O];

b) [C, SO, B].

Trả lời

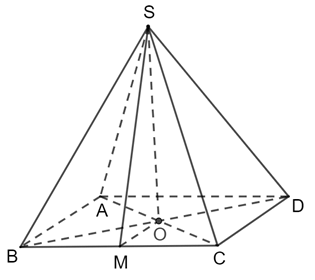
a) Gọi M là trung điểm BC.

ΔSBC đều ⇒ SM ⊥ BC

ΔOBC vuông cân tại O ⇒ OM ⊥ BC

Khi đó góc phẳng nhị diện [S, BC, O] = (MO, MS).

Ta có: O là trung điểm của BD, M là trung điểm của BC

⇒ OM là đường trung bình của ΔBCD

$\Rightarrow \mathrm{OM}=\frac{1}{2}\mathrm{CD}=\frac{a}{2}$

$\mathrm{AC}=\sqrt{{\mathrm{AB}}^2+{\mathrm{BC}}^2}=a\sqrt{2}\Rightarrow \mathrm{OC}=\frac{\mathrm{AC}}{2}=\frac{a\sqrt{2}}{2}$

ΔSBC đều, M là trung điểm của BC

⇒ SM là đường trung tuyến $\Rightarrow \mathrm{SM}=\frac{a\sqrt{3}}{2}$

$\cos \left(\mathrm{MO},\mathrm{MS}\right)=\frac{\mathrm{OM}}{M\text{S}}=\frac{\frac{a}{2}}{\frac{a\sqrt{3}}{2}}=\frac{a}{2}.\frac{2}{a\sqrt{3}}=\frac{1}{\sqrt{3}}$.

Suy ra [S, BC, O] = (MO, MS) $\approx 54°7\text{'}$

b) Ta có:

• SO ⊥ (ABCD) nên SO⊥OB

• SO ⊥ (ABCD) nên SO⊥OC

Vậy $\widehat{\mathrm{BOC}}$ là góc phẳng nhị diện [C, SO, B].

Mà ABCD là hình vuông nên $\widehat{\mathrm{BOC}}=90°$.
Vậy [C, SO, B] = 90^o.

Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác: