Giải SGK Toán 11 (Chân trời sáng tạo) Bài tập cuối chương 8

Giải Toán 11 Bài tập cuối chương 8

Câu hỏi trắc nghiệm

Bài 1 trang 86 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với mặt đáy. Đường thẳng CD vuông góc với mặt phẳng nào sau đây?

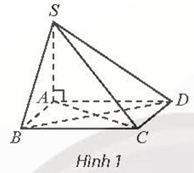
A. (SAD).

B. (SAC).

C. (SAB).

D. (SBD).

Lời giải:

Đáp án đúng là: A

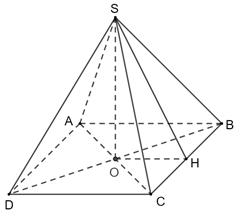
Vì SA ⊥ (ABCD) nên SA ⊥ CD.

Mà ABCD là hình vuông nên CD ⊥ AD.

Do đó CD ⊥ (SAD).

Bài 2 trang 86 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh b, SA vuông góc với mặt đáy, $\text{SC=2b}\sqrt{2}$. Số đo góc giữa cạnh bên SC và mặt đáy là

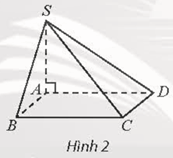
A. 60°.

B. 30°.

C. 45°.

D. 50°.

Lời giải:

Đáp án đúng là: A

Ta có SA ⊥ (ABCD) suy ra (SC, (ABCD)) = (SC, AC) = $\widehat{\mathrm{SCA}}$

Mà ABCD là hình vuông nên $\mathrm{AC}=\sqrt{{\mathrm{AB}}^2+{\mathrm{BC}}^2}=b\sqrt{2}$

$\cos \widehat{\mathrm{SCA}}=\frac{\mathrm{AC}}{\mathrm{SC}}=\frac{1}{2}\Rightarrow \widehat{\mathrm{SCA}}=60°$.

Vậy (SC, (ABCD)) = 60°

Bài 3 trang 86 Toán 11 Tập 2: Cho hình chóp S.ABCD có các cạnh bên và cạnh đáy đều bằng a. Gọi M là trung điểm của SA. Mặt phẳng (MBD) vuông góc với mặt phẳng nào dưới đây?

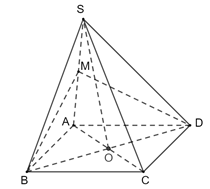
A. (SBC).

B. (SAC).

C. (SBD).

D. (ABCD).

Lời giải:

Đáp án đúng là: B

Gọi O là tâm của đáy.

Khi đó SO ⊥ (ABCD) nên SO ⊥ BD

Vì ABCD là hình vuông nên AC ⊥ BD. Khi đó:

$\left.\begin{array}{c}\mathrm{BD}\perp \left(\mathrm{SAC}\right)\\ \mathrm{BD}\subset \left(\mathrm{MBD}\right) \end{array}\right\}\Rightarrow \left(\text{MBD}\right)\perp \left(\text{SAC}\right)$

Bài 4 trang 86 Toán 11 Tập 2: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng và chiều cao bằng $a\sqrt{2}$. Khoảng cách từ tâm O của đáy ABC đến một mặt bên là

A. $\frac{a\sqrt{14}}{7}$ .

B. $\frac{a\sqrt{2}}{7}$ .

C. $\frac{a\sqrt{14}}{2}$ .

D. $\frac{2a\sqrt{14}}{7}$ .

Lời giải:

Đáp án đúng là: A

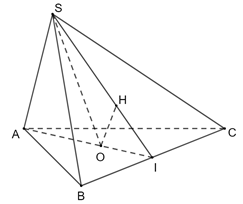
Gọi I là trung điểm của BC, kẻ OH ⊥ SI (H $\in$ SI).

Vì ΔABC là tam giác đều nên AI ⊥ BC

Ta có: SO⊥(ABC) nên SO⊥BC

⇒ BC ⊥ (SAI) ⇒ BC ⊥ OH

Mà OH ⊥ SI nên OH ⊥ (SBC)

Do đó d(O, (SBC)) = OH

ΔABC là tam giác đều $\Rightarrow \mathrm{AI}=a\sqrt{3}\Rightarrow \mathrm{OI}=\frac{1}{3}\mathrm{AI}=\frac{a\sqrt{3}}{3}$

ΔOHI vuông tại O, OH là đường cao:

$\frac{1}{{\mathrm{OH}}^2}=\frac{1}{{\mathrm{SO}}^2}+\frac{1}{{\mathrm{OI}}^2}\Rightarrow \mathrm{OH}=\frac{a\sqrt{14}}{7}$

Bài 5 trang 86 Toán 11 Tập 2: Thể tích của khối chóp cụt tam giác đều có cạnh đáy lớn bằng 2a, cạnh đáy nhỏ bằng a và chiều cao bằng $\frac{a\sqrt{6}}{3}$ là

A. $\frac{7\sqrt{2}}{8}{a}^3$ .

B. $\frac{\sqrt{2}}{4}{a}^3$ .

C. $\frac{7\sqrt{2}}{12}{a}^3$ .

D. $\frac{7\sqrt{3}}{4}{a}^3$ .

Lời giải:

Đáp án đúng là: C

Diện tích đáy lớn là: $S=\frac{{\left(2a\right)}^2\sqrt{3}}{4}=a^2\sqrt{3}$

Diện tích đáy bé là: $S\text{'}=\frac{a^2\sqrt{3}}{4}$

Thể tích của bồn chứa là:

$V=\frac{1}{3}\cdot \frac{a\sqrt{6}}{3}\cdot \left(a^2\sqrt{3}+\sqrt{a^2\sqrt{3}\cdot \frac{a^2\sqrt{3}}{4}}+\frac{a^2\sqrt{3}}{4}\right)=\frac{7\sqrt{2}}{12}{a}^3$.

Bài 6 trang 86 Toán 11 Tập 2: Cho chóp tứ giác S.ABCD có đáy là hình chữ nhật với AB = 4a, AD = 3a. Các cạnh bên đều có độ dài 5a. Góc nhị diện [S, BC, A] có số đo là

A. 75°46′.

B. 71°21′.

C. 68°31′.

D. 65°12′.

Lời giải:

Đáp án đúng là: D

Gọi O là tâm của đáy.

Kẻ OH ⊥ BC (H $\in$ BC)

Vì ΔSAC cân tại S nên SO ⊥ AC.

Vì ΔSBD cân tại S nên SO ⊥ BD.

⇒ SO ⊥ (ABCD) ⇒ SO ⊥ BC.

Mà OH ⊥ BC nên $\widehat{\mathrm{SHO}}$ là góc nhị diện [S, BC, A].

$S_{\mathrm{ABCD}}=\mathrm{AB}.\mathrm{AD}=12a^2\Rightarrow {\text{S}}_{\text{OBC}}=\frac{1}{4}{S}_{\mathrm{ABCD}}=3a^2$.

Mà $S_{\mathrm{OBC}}=\frac{1}{2}.\mathrm{BC}.\mathrm{OH}\Rightarrow \mathrm{OH}=\frac{2S_{\mathrm{OBC}}}{\mathrm{BC}}=2a$.

• $\mathrm{AC}=\sqrt{{\mathrm{AB}}^2+{\mathrm{BC}}^2}=5a\Rightarrow \mathrm{OC}=\frac{1}{2}\mathrm{AC}=\frac{5a}{2}$.

• $\mathrm{SO}=\sqrt{{\mathrm{SC}}^2-{\mathrm{OC}}^2}=\frac{5a\sqrt{3}}{2}$.

• $\tan \widehat{\mathrm{SHO}}=\frac{\mathrm{SO}}{\mathrm{OH}}=\frac{5\sqrt{3}}{4}\Rightarrow \widehat{\mathrm{SHO}}\approx 65°12\text{'}$.

Bài 7 trang 86 Toán 11 Tập 2: Nếu hình hộp chữ nhật có ba kích thước là 3, 4, 5 thì độ dài đường chéo của nó là

A. $5\sqrt{2}$ .

B. 50.

C. $2\sqrt{5}$ .

D. 12.

Lời giải:

Đáp án đúng là: A

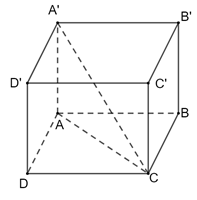
Giả sử hình hộp chữ nhật ABCD.A′B′C′D′ có AB = 3, BC = 4, AA′ = 5.

• $\mathrm{AC}=\sqrt{{\mathrm{AB}}^2+{\mathrm{BC}}^2}=5$.

• $A^{\text{'}}C=\sqrt{A{A^{\text{'}}}^2+{\mathrm{AC}}^2}=5\sqrt{2}$.

Bài 8 trang 86 Toán 11 Tập 2: Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a là

A. $\frac{a^3\sqrt{3}}{4}$ .

B. $\frac{a^3\sqrt{3}}{3}$ .

C. $\frac{a^3\sqrt{2}}{3}$ .

D. $\frac{a^3\sqrt{2}}{2}$ .

Lời giải:

Đáp án đúng là: A

Diện tích đáy của khối lăng trụ là: $S=\frac{a^2\sqrt{3}}{4}$.

Chiều cao của khối lăng trụ là cạnh bên của lăng trụ bằng: h = a.

Thể tích của khối lăng trụ là: $V=Sh=\frac{a^2\sqrt{3}}{4}.a=\frac{a^3\sqrt{3}}{4}$.

Bài tập tự luận

Bài 9 trang 86 Toán 11 Tập 2: Cho hình vuông ABCD và tam giác đều SAB cạnh a nằm trong hai mặt phẳng vuông góc với nhau. Gọi M,N lần lượt là trung điểm của AB và AD.

a) Chứng minh rằng $\left(\mathrm{SMD}\right)\perp \left(\mathrm{SNC}\right)$.

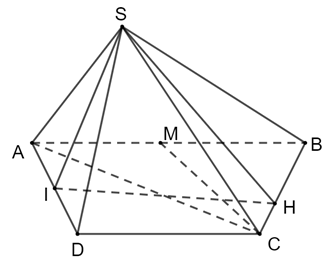
b) Tính khoảng cách từ M đến mặt phẳng (SNC).

Lời giải:

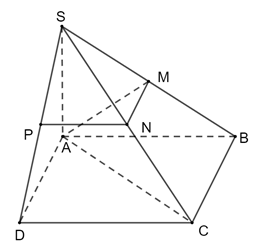
a) Tam giác SAB đều có M là trung điểm AB nên SM ⊥ AB. Mà (SAB) ⊥ (SAB) nên SM ⊥ (ABCD). Suy ra SM ⊥ NC.

Xét ΔAMD và ΔDNC

AM = DN

$\widehat{\mathrm{MAD}}=\widehat{\mathrm{NDC}}$

AD = DC

Do đó ΔAMD và ΔDNC (c.g.c)

Suy ra $\widehat{\mathrm{AM}\text{D}}=\widehat{\mathrm{CN}\text{D}}$ (hai góc tương ứng)

Mà $\widehat{\mathrm{AM}\text{D}}+\widehat{A\text{DM}}=90°$ nên $\widehat{\text{CND}}+\widehat{A\text{DM}}=90°$.

Từ đó ta có tam giác DNI vuông tại I hay DM ⊥ NC. Mà SM ⊥ NC nên NC ⊥ (SND).

Vậy (SNC) ⊥ (SMD).

b) Kẻ MH ⊥ SI (H $\in$ SI).

Vì NC ⊥ (SMD) ⇒ NC ⊥ MH ⇒ MH ⊥ (SNC)

Tam giác SAB đều có SM là trung tuyến nên $\mathrm{SM}=\frac{a\sqrt{3}}{2}$

Tam giác CND vuông có DI là đường cao nên $\frac{1}{{\mathrm{DI}}^2}=\frac{1}{{\mathrm{DN}}^2}+\frac{1}{{\mathrm{DC}}^{2^{}}}$.

Suy ra $\mathrm{DI}=\frac{a\sqrt{5}}{5}$

• $\mathrm{DM}=\sqrt{{\mathrm{AM}}^2+A{\text{D}}^{2^{}}}=\frac{a\sqrt{5}}{5}$

• $\mathrm{MI}=M\text{D}-\mathrm{DI}=\frac{3\text{a}\sqrt{5}}{10}$

Và SM ⊥ (ABCD) nên SM ⊥ MI.

Tam giác SMI vuông tại M có MH là đường cao

$\frac{1}{{\mathrm{MH}}^2}=\frac{1}{{\mathrm{SM}}^2}+\frac{1}{{\mathrm{MI}}^{2^{}}}\Rightarrow \mathrm{MH}=\frac{3\text{a}\sqrt{2}}{8}$

Bài 10 trang 87 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (ABCD) và SA = a. Gọi M, N, P lần lượt là trung điểm của SB, SC và SD. Tính khoảng cách giữa AM và NP.

Lời giải:

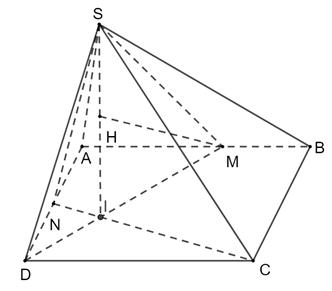
Vì SA ⊥ (ABCD) nên SA ⊥ BC

Mà BC ⊥ AB nên BC ⊥ (SAB)

Tam giác SBC có:

M là trung điểm SB

N là trung điểm SC

Do đó MN là đường trung bình nên MN // BC, $\mathrm{MN}=\frac{1}{2}\mathrm{BC}=\frac{a}{2}$ .

Mà BC ⊥ (SAB) ⇒ MN ⊥ (SAB) ⇒ MN ⊥ AM.

Tam giác SCD cóN là trung điểm SC; P là trung điểm SD

Suy ra P là đường trung bình nên NP // CD.

Mà MN // BC, BC ⊥ CD nên MN ⊥ NP.

Vậy: $d(\mathrm{AM},\mathrm{NP})=\mathrm{MN}=\frac{a}{2}$

Bài 11 trang 87 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = AD = 2a, CD = a; số đo góc nhị diện [S, BC, A] bằng 60°. Gọi I là trung điểm của cạnh AD. Biết hai mặt phẳng (SBI) và (SCI) cùng vuông góc với mặt phẳng (ABCD). Tính thể tích khối chóp S.ABCD theo a.

Lời giải:

Kẻ IH ⊥ BC

Ta có:

$\left.\begin{array}{l}\left(\mathrm{SIB}\right)\perp \left(\mathrm{ABC}\text{D}\right)\\ \left(\mathrm{SIC}\right)\perp \left(\mathrm{ABC}\text{D}\right)\\ \left(\mathrm{SIB}\right)\cap \left(\mathrm{SIC}\right)=\mathrm{SI}\end{array}\right\}\Rightarrow \mathrm{SI}\perp (ABCD)$

Suy ra: SI ⊥ BC mà BC ⊥ IH ⇒ BC ⊥ (SHI) $\Rightarrow$ BC ⊥ SH.

Lại có: $[S,\mathrm{BC},A]=\widehat{\mathrm{SHI}}=60°$.

$S_{\mathrm{ABC}\text{D}}=\frac{1}{2}\left(\mathrm{AB}+\mathrm{CD}\right)\mathrm{AD}=3a^2$;

Ta có: I là trung điểm AD $\Rightarrow$ $\mathrm{AI}=\mathrm{ID}=\frac{1}{2}\mathrm{AD}=a$.

${\mathrm{S}}_{\mathrm{ABI}}=\frac{1}{2}.\mathrm{AB}.\mathrm{AI}={\mathrm{a}}^2$

${\mathrm{S}}_{\mathrm{I}\text{D}\mathrm{C}}=\frac{1}{2}.\mathrm{CD}.\mathrm{ID}=\frac{{\mathrm{a}}^2}{2}$

${\mathrm{S}}_{\mathrm{IBC}}={\mathrm{S}}_{\mathrm{ABCD}}-{\mathrm{S}}_{\mathrm{AIB}}-{\mathrm{S}}_{\mathrm{CID}}=\frac{3{\text{a}}^2}{2}$

Gọi M là trung điểm của AB.

$\Rightarrow \mathrm{BM}=\frac{1}{2}\mathrm{AB}=a$, CM = AD = 2a $\Rightarrow \mathrm{BC}=\sqrt{{\mathrm{BM}}^2+{\mathrm{CM}}^2}=a\sqrt{5}$ ;

$\Rightarrow \mathrm{IH}=\frac{2S_{\mathrm{IBC}}}{\mathrm{BC}}=\frac{3\text{a}\sqrt{5}}{5}$ $\Rightarrow \mathrm{SI}=\mathrm{IH}.\tan 60°=\frac{3a\sqrt{15}}{5}$.

Vậy $V_{S.\mathrm{ABC}\text{D}}=\frac{1}{3}.\mathrm{SI}.S_{\mathrm{ABC}\text{D}}=\frac{3{\text{a}}^3\sqrt{15}}{5}$.

Bài 12 trang 87 Toán 11 Tập 2: Một chân cột bằng gang có dạng hình chóp cụt tứ giác đều có cạnh đáy lớn bằng 2a, cạnh đáy nhỏ bằng a, chiều cao h = 2a và bán kính đáy phần trụ rỗng bên trong bằng $\frac{a}{2}$.

a) Tìm góc phẳng nhị diện tạo bởi mặt bên và mặt đáy.

b) Tính thể tích chân cột nói trên theo a.

Lời giải:

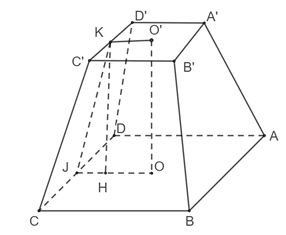
Mô hình hoá chân cột bằng gang bằng cụt chóp tứ giác đều ABCD.A′B′C′D′ với O, O′ là tâm của hai đáy. Vậy AB = 2a, A′B′ = a, OO′ = 2a.

a) Gọi J, K lần lượt là trung điểm của CD, C′D′.

• A′B′C′D′ là hình vuông nên O′K ⊥ C′D′.

• CDD′C′ là hình thang cân nên JK ⊥ C′D.

Vậy $\widehat{\mathrm{JKO}\text{'}}$ là góc phẳng nhị diện giữa mặt bên và đáy nhỏ, $\widehat{\mathrm{KJO}}$ là góc phẳng nhị diện giữa mặt bên và đáy lớn.

b) Diện tích đáy lớn là: $S=A{B}^2=4a^2$.

Diện tích đáy bé là: $S\text{'}=A^{\text{'}}{B}^{\text{'}2}=a^2$.

Thể tích hình chóp cụt là:

${\text{V}}_1=\frac{1}{3}h\left(S+\sqrt{{\mathrm{SS}}^{\text{'}}}+S^{\text{'}}\right)=\frac{14a^3}{3}$.

Thể tích hình trụ rỗng là: $V_2={\mathrm{\pi R}}^{2}h=\frac{{\mathrm{\pi a}}^3}{2}$.

Thể tích chân cột là: $V=V_1-V_2=\left(\frac{14}{3}-\frac{\pi }{2}\right)a^3$.

Bài 13 trang 87 Toán 11 Tập 2: Cho hình hộp ABCD.A′B′C′D′ có cạnh bên AA′ = a, đáy ABCD là hình thoi có AB = BD = a. Hình chiếu vuông góc của A′ lên mặt đáy trùng với điểm O là giao điểm hai đường chéo của đáy. Tính thể tích của khối hộp.

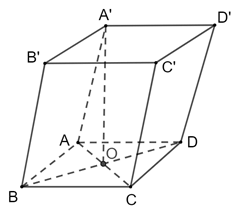
Lời giải:

Xét tam giác ABD có AB = BD = AD = a nên ΔABD đều

Suy ra $\widehat{\mathrm{BAD}}=60°$

ABCD là hình thoi, O là trung điểm của BD

$\Rightarrow \mathrm{BO}=\frac{1}{2}\mathrm{BD}=\frac{a}{2},\mathrm{AO}=\sqrt{{\mathrm{AB}}^2-{\mathrm{BO}}^2}=\frac{a\sqrt{3}}{2}$.

Ta có: AA′ ⊥ (ABCD) $\Rightarrow$ AA′ ⊥ AO .

$\Rightarrow A^{\text{'}}O=\sqrt{{\mathrm{AA}}^{\text{'}2}-{\mathrm{AO}}^2}=\frac{a}{2}$

$S_{\mathrm{ABCD}}=\mathrm{AB}.\mathrm{AD}.\sin \widehat{\mathrm{BAD}}=\frac{a^2\sqrt{3}}{2}$

$V_{\mathrm{ABCD}.A\text{'}B\text{'}C\text{'}D\text{'}}=A\text{'}O.S_{\mathrm{ABCD}}=\frac{a^3\sqrt{3}}{4}$

Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác: