Cho hình chóp tứ giác đều S.ABCD có O là tâm của đáy và có tất cả các cạnh bằng nhau

Bài 2 trang 85 Toán 11 Tập 2: Cho hình chóp tứ giác đều S.ABCD có O là tâm của đáy và có tất cả các cạnh bằng nhau.

a) Tìm góc giữa đường thẳng SA và (ABCD).

b) Tìm góc phẳng nhị diện [A, SO, B], [S, AB, O].

Trả lời

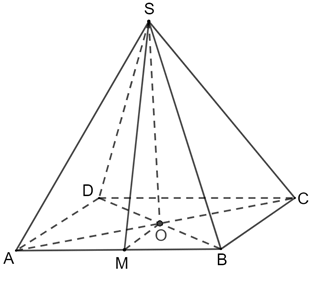
a) S.ABCD là hình chóp tứ giác đều có O là tâm của đáy

$\Rightarrow$ SO ⊥ (ABCD) ⇒ (SA, (ABCD)) = (SA,OA) = $\widehat{\mathrm{SAO}}$

Vậy góc giữa đường thẳng SA và (ABCD) là $\widehat{\mathrm{SAO}}$

b) Gọi M là trung điểm của AB

SO ⊥ (ABCD) ⇒ SO ⊥ AO, SO ⊥ BO

Vậy $\widehat{\mathrm{AOB}}$ là góc phẳng nhị diện [A, SO, B]

• ABCD là hình vuông nên $\widehat{\mathrm{AOB}}=90°$

• ΔSAB đều nên SM ⊥ AB

• ΔOAB vuông cân tại O nênOM ⊥ AB

Vậy $\widehat{\mathrm{SMO}}$ là góc phẳng nhị diện [S, AB, O].

Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác: