Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, K lần lượt là trung điểm của các cạnh AB, BC, SA. Biết mặt phẳng ( MNK) chia khối chóp (S.ABCD) thành hai phần có thể tích là V1,
34
04/05/2024
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(M\), \(N\), \(K\) lần lượt là trung điểm của các cạnh \(AB\), \(BC\), \(SA\). Biết mặt phẳng \(\left( {MNK} \right)\) chia khối chóp \(S.ABCD\) thành hai phần có thể tích là \({V_1},{V_2}\) \(\left( {{V_1} < {V_2}} \right)\). Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\).
A. \(\frac{7}{{13}}\).
B. \(\frac{9}{{23}}\).
C. \(\frac{{49}}{{71}}\).
D. \(\frac{{17}}{{67}}\).
Trả lời
Lời giải
Chọn B
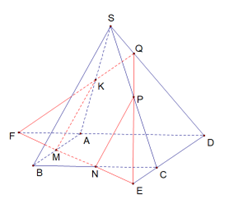
Trong mặt phẳng \(\left( {ABCD} \right)\), kéo dài \(MN\) cắt \(DA\), \(DC\) lần lượt tại \(F\), \(E\).
Trong mặt phẳng \(\left( {SAD} \right)\), gọi \(FK \cap SD = Q\). Trong mặt phẳng \(\left( {SCD} \right)\), gọi \(QE \cap SC = P\).
Suy ra thiết diện là ngũ giác \(MNPQK\) và \(MN{\rm{//}}AC\;{\rm{//\;}}PK\).
Đặt \(h = d\left( {S,\left( {ABCD} \right)} \right)\) \( \Rightarrow d\left( {K,\left( {ABCD} \right)} \right) = d\left( {P,\left( {ABCD} \right)} \right) = \frac{1}{2}h\)
Ta có: \(FA = BN = \frac{1}{2}AD \Rightarrow \frac{{FD}}{{FA}} = 3\).
Áp dụng định lý Menelaus cho tam giác \(SAD\), suy ra
\(\frac{{QS}}{{QD}}.\frac{{FD}}{{FA}}.\frac{{KA}}{{KS}} = 1 \Rightarrow \frac{{QS}}{{QD}} = \frac{1}{3} \Rightarrow \frac{{QD}}{{SD}} = \frac{3}{4} \Rightarrow d\left( {Q,\left( {ABCD} \right)} \right) = \frac{3}{4}h\)
Mặt khác: \({S_{FAM}} = {S_{NCE}} = {S_{BMN}} = \frac{1}{4}{S_{ABC}} = \frac{1}{8}{S_{ABCD}} \Rightarrow {S_{DEF}} = \frac{9}{8}{S_{ABCD}}\)
Suy ra thể tích của khối đa diện không chứa đỉnh S là
\(V = {V_{QDEF}} - {V_{KAMF}} - {V_{PECN}} = \frac{1}{3}\left( {\frac{3}{4}h.\frac{9}{8}S - \frac{1}{2}h.\frac{1}{8}S - \frac{1}{2}h.\frac{1}{8}S} \right)\)
\( = \frac{1}{3}.\frac{{23}}{{32}}.h.{S_{ABCD}} = \frac{{23}}{{32}}{V_{ABCD}} = {V_2}\)
\( \Rightarrow {V_1} = \frac{9}{{32}} \Rightarrow \frac{{{V_1}}}{{{V_2}}} = \frac{9}{{23}}\)

