Cho hàm số y = f( x ). Hàm số y = f'( x )có đồ thị là đường parabol như hình vẽ. Hàm số y = f( 1 - x^2) + 6x^2 đồng biến trên khoảng nào dưới đây? A. ( 1; căn bậc hai của 2). B. ( c
50
04/05/2024
Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\)có đồ thị là đường parabol như hình vẽ. Hàm số \(y = f\left( {1 - {x^2}} \right) + 6{x^2}\)đồng biến trên khoảng nào dưới đây?
A. \(\left( {1;\sqrt 2 } \right)\).
B. \(\left( {\sqrt 2 ; + \infty } \right)\).
C. \(\left( { - \sqrt 2 ;0} \right)\).
D. \(\left( { - \infty ; - 1} \right)\).
Trả lời
Lời giải
Chọn A
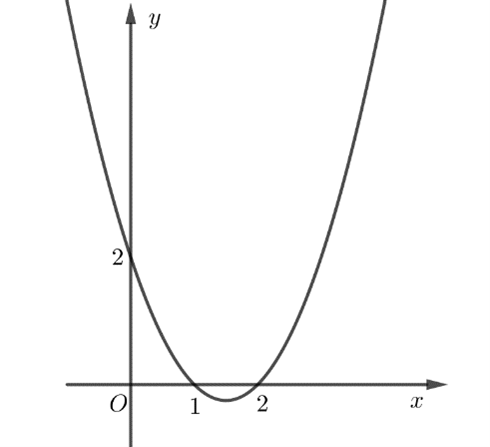
Đồ thị hàm số \(y = f'\left( x \right)\)đi qua 3 điểm \(\left( {2;0} \right)\), \(\left( {1;0} \right)\), \(\left( {0;2} \right)\)nên hàm số \(y = f'\left( x \right)\)có dạng\(y = f'\left( x \right) = {x^2} - 3x + 2\).
Xét hàm số \(y' = {\left[ {f\left( {1 - {x^2}} \right) + 6{x^2}} \right]^'} = - 2xf'\left( {1 - {x^2}} \right) + 12x\)
\( = - 2x\left[ {{{\left( {1 - {x^2}} \right)}^2} - 3\left( {1 - {x^2}} \right) + 2} \right] + 12x = - 2x\left( {{x^4} + {x^2} - 6} \right) = - 2x\left( {{x^2} - 2} \right)\left( {{x^2} + 3} \right)\).
Bảng biến thiên của hàm số \(y = f\left( {1 - {x^2}} \right) + 6{x^2}\).
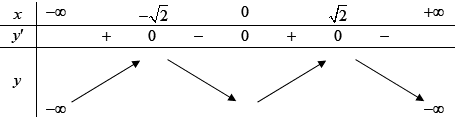
Hàm số đồng biến trên khoảng \(\left( { - \infty ; - \sqrt 2 } \right)\)và\(\left( {0;\sqrt 2 } \right) \Rightarrow \) hàm số \(y = f\left( {1 - {x^2}} \right) + 6{x^2}\)đồng biến trên khoảng \(\left( {1;\sqrt 2 } \right)\).


