Cho hàm số f( x ) xác định và liên tục trên R { - 1} có bảng biến thiên như sau: Hỏi đồ thị hàm số y = 1/f( x ) có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang? A. 1 B.
39
04/05/2024
Cho hàm số \(f\left( x \right)\)xác định và liên tục trên \(\mathbb{R}\backslash \left\{ { - 1} \right\}\)có bảng biến thiên như sau:
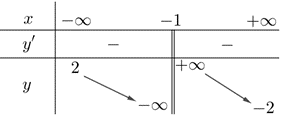
Hỏi đồ thị hàm số \(y = \frac{1}{{f\left( x \right)}}\)có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
A. \(1\).
B. \(3\).
C. \(2\).
D. \(4\).
Trả lời
Lời giải
Chọn D
Ta có: \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 2 \Rightarrow \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{f\left( x \right)}} = \frac{1}{2}\); \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = - 2 \Rightarrow \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{f\left( x \right)}} = - \frac{1}{2}\).
Suy ra đồ thị hàm số \(y = \frac{1}{{f\left( x \right)}}\)có hai đường tiệm cận ngang là \(y = \frac{1}{2}\)và \(y = - \frac{1}{2}\).
Dựa vào bảng biến thiên của hàm số \(y = f\left( x \right)\)ta thấy: phương trình \(f\left( x \right) = 0\)có hai nghiệm phân biệt \({x_1} < - 1 < {x_2}\).
Khi đó: \(f\left( {{x_1}} \right) = f\left( {{x_2}} \right) = 0\).
Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {x_1}^ - } f\left( x \right) = 0\\f\left( x \right) > 0\,khi\,x \to {x_1}^ - \end{array} \right. \Rightarrow \mathop {\lim }\limits_{x \to {x_1}^ - } \frac{1}{{f\left( x \right)}} = + \infty \)và \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {x_2}^ - } f\left( x \right) = 0\\f\left( x \right) > 0\,khi\,x \to {x_2}^ - \end{array} \right. \Rightarrow \mathop {\lim }\limits_{x \to {x_2}^ - } \frac{1}{{f\left( x \right)}} = + \infty \).
Vậy đồ thị hàm số \(y = \frac{1}{{f\left( x \right)}}\)có hai tiệm cận đứng là đường thẳng \(x = {x_1}\)và \(x = {x_2}\).

