Dạng 1: Cách làm các bài tập giải tam giác có đáp án
-
191 lượt thi
-
12 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Xem đáp án
Hướng dẫn giải:
Từ định lí tổng 3 góc trong tam giác, ta có \(\widehat A = 180^\circ - \left( {\widehat B + \widehat C} \right) = 70^\circ \).
Theo định lí sin, ta có \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{b = \frac{{a.\sin B}}{{\sin A}} = \frac{{10.\sin 50^\circ }}{{\sin 70^\circ }} \approx 8,15}\\{c = \frac{{a.\sin C}}{{\sin A}} = \frac{{10.\sin 60^\circ }}{{\sin 70^\circ }} \approx 9,22}\end{array}} \right.\).
Câu 2:
Xem đáp án
Hướng dẫn giải:
Theo hệ quả của định lí côsin, ta có:
\(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{8^2} + {9^2} - {7^2}}}{{2.8.9}} = \frac{2}{3} \Rightarrow \widehat A \approx 48^\circ 11'\).
\(\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}} = \frac{{{7^2} + {9^2} - {8^2}}}{{2.7.9}} = \frac{{11}}{{21}} \Rightarrow \widehat B \approx 58^\circ 24'\).
Do đó \(\widehat C = 180^\circ - \left( {\widehat A + \widehat B} \right) \approx 73^\circ 25'\).
Câu 3:
Tam giác ABC có b = 12, c = 15, \(\widehat A = 140^\circ \). Khi đó, tìm khẳng định sai trong các khẳng định dưới đây?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Theo định lý côsin ta có: \({a^2} = {b^2} + {c^2} - 2bc.\cos A\).
Thay số ta được: \({a^2} = {12^2} + {15^2} - 2.12.15.\cos 140^\circ \approx 644,76\)
⇒ a ≈ 25,4.
Lại có: \(\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}} \approx \frac{{{{25,4}^2} + {{15}^2} - {{12}^2}}}{{2.25,4.15}} \approx 0,95\)
\( \Rightarrow \widehat B \approx 17,64^\circ \).
Từ đó, \(\widehat C = 180^\circ - \left( {\widehat A + \widehat B} \right) \approx 180^\circ - \left( {140^\circ + 17,64^\circ } \right) = 22,36^\circ \).
Câu 4:
Cho tam giác ABC biết a = 3, b = 5, c = 7. Tìm khẳng định đúng trong các khẳng định sau?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Áp dụng hệ quả của định lí côsin, ta có: \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{5^2} + {7^2} - {3^2}}}{{2.5.7}} = \frac{{13}}{{14}}\)
\( \Rightarrow \widehat A \approx 21,79^\circ \)
Ta có: \(\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}} = \frac{{{3^2} + {7^2} - {5^2}}}{{2.3.7}} = \frac{{11}}{{14}}\).
\( \Rightarrow \widehat B \approx 38,21^\circ \).
Do đó: \(\widehat C = 180^\circ - \left( {\widehat A + \widehat B} \right) \approx 180^\circ - \left( {21,79^\circ + 38,21^\circ } \right) = 120^\circ \).
Câu 5:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Áp dụng định lý côsin ta có:
\(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)\( \Leftrightarrow \frac{1}{2} = \frac{{{b^2} + {{12}^2} - {{16}^2}}}{{2.b.12}}\)\[ \Leftrightarrow 2{b^2} - 224 = 24b\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{b = 6 + 2\sqrt {37} }\\{b = 6 - 2\sqrt {37} \,\,\,(loai)}\end{array}} \right.\).
Vậy b = 6 + 2\(\sqrt {37} \).
Lại có: \(\frac{a}{{\sin A}} = \frac{c}{{\sin C}}\)\( \Rightarrow \sin C = \frac{{\sin A.c}}{a} = \frac{{\sin 60^\circ .12}}{{16}} = \frac{{3\sqrt 3 }}{8}\).
\( \Rightarrow \widehat C \approx 40,5^\circ \).
Vậy \(\widehat B = 180^\circ - \left( {\widehat A + \widehat C} \right) \approx 180^\circ - \left( {60^\circ + 40,5^\circ } \right) = 79,5^\circ \).
Câu 6:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Trong tam giác ABC:
\(\widehat A = 180^\circ - \left( {\widehat B + \widehat C} \right) \approx 180^\circ - \left( {43^\circ 42' + 16^\circ 20'} \right) = 119^\circ 58'\).
Theo định lý sin ta có:
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)
\( \Rightarrow b = \frac{{a.\sin B}}{{\sin A}} \approx \frac{{46.\sin 43^\circ 42'}}{{\sin 119^\circ 58'}} \approx 36,68\).
Và \(c = \frac{{a.\sin C}}{{\sin A}} \approx \frac{{46.\sin 16^\circ 20'}}{{\sin 119^\circ 58'}} \approx 14,93\).
Câu 7:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Ta có: \(\widehat B = 180^\circ - \left( {\widehat A + \widehat C} \right) = 180^\circ - \left( {90^\circ + 23^\circ } \right) = 67^\circ \).
Lại có: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)
\( \Rightarrow b = \frac{{a.\sin B}}{{\sin A}} = 20.\sin 67^\circ \approx 18,41\).
Và \(c = \frac{{a.\sin C}}{{\sin A}} = 20.\sin 23^\circ \approx 7,81\).
Câu 8:
Cho tam giác ABC biết AB = 3, \(AC = 3\sqrt 2 \) và \(\widehat C = 45^\circ \). Trong các phương án dưới đây, chọn phương án SAI?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Ta có: \(A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos 45^\circ \)
\( \Leftrightarrow {3^2} = {\left( {3\sqrt 2 } \right)^2} + B{C^2} - 2.BC.3\sqrt 2 .\frac{{\sqrt 2 }}{2}\)
\( \Leftrightarrow B{C^2} - 6BC + 9 = 0\)
⇔ (BC – 3)2 = 0
⇒ BC = 3.
Dễ thấy AB2 + BC2 = AC2 nên theo định lý đảo của định lý Pythagore suy ra tam giác ABC vuông tại B.
Vậy \(\widehat B = 90^\circ \), \(\widehat A = 45^\circ \).
Câu 9:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Từ AB : AC = 3 : 4\( \Rightarrow \frac{{AB}}{3} = \frac{{AC}}{4}\).
Đặt \(\frac{{AB}}{3} = \frac{{AC}}{4} = k\), k > 0 ⇒ AB = 3k; AC = 4k.
Ta có: \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\)\( \Leftrightarrow \frac{1}{{{{24}^2}}} = \frac{1}{{9{k^2}}} + \frac{1}{{16{k^2}}}\)\( \Leftrightarrow \)k = 10.
Suy ra: AB = 30; AC = 40, từ đó suy ra BC = 50 (định lí Pythagore).
Lại có: cos B = \[\frac{{AB}}{{BC}} = \frac{{30}}{{50}} = \frac{3}{5}\]\( \Rightarrow \widehat B \approx 53,13^\circ \)
\( \Rightarrow \widehat C = 90^\circ - \widehat B \approx 36,87^\circ \).
Câu 10:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Ta có: cos A = \(\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)= \(\frac{{{{17}^2} + {{20}^2} - {{16}^2}}}{{2.17.20}}\)= \(\frac{{433}}{{680}}\)
\( \Rightarrow \widehat A\)= 50,45\(^\circ \).
Tương tự: cos B = \(\frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\)= \(\frac{{{{16}^2} + {{20}^2} - {{17}^2}}}{{2.16.20}}\)= \(\frac{{367}}{{640}}\)
\( \Rightarrow \widehat B \approx 55^\circ \)
Do đó: \(\widehat C = 180^\circ - \left( {\widehat A + \widehat B} \right) \approx 180^\circ - \left( {50,45^\circ + 55^\circ } \right) = 74,55^\circ \).
Câu 11:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Trong tam giác ABC có: \(\widehat B = 180^\circ - \left( {\widehat A + \widehat C} \right) = 180^\circ - \left( {30^\circ + 45^\circ } \right) = 105^\circ \).
Theo định lý sin ta có: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)
Do đó: a = \(\frac{{c.sinA}}{{\sin C}}\)= \(\frac{{7,2.\sin 30^\circ }}{{\sin 45^\circ }}\)= \(\frac{{18\sqrt 2 }}{5}\).
Và b = \(\frac{{c.\sin B}}{{\sin C}}\)= \(\frac{{7,2.\sin 105^\circ }}{{\sin 45^\circ }}\)= \(\frac{{18 + 18\sqrt 3 }}{5}\).
Câu 12:
Cho hình thoi ABCD có cạnh bằng 2 cm và \(\widehat {ABC} = 60^\circ \). Tìm khẳng định SAI trong các khẳng định sau?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
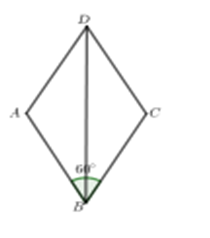
Vì \(\widehat {ABC} = 60^\circ \) nên \(\widehat {BAD} = 120^\circ \).
Ta có ABCD là hình thoi nên AB = AD = 2 cm.
Lại có BD là tia phân giác của góc \(\widehat {ABC}\) nên \(\widehat {ABD} = \frac{1}{2}\widehat {ABC} = \frac{1}{2}.60^\circ = 30^\circ \).
Mà AB = AD nên tam giác ABD cân tại A.
Do đó: \(\widehat {ADB} = \widehat {ABD} = 30^\circ \) và \(\widehat {BAD} = 180^\circ - 2\widehat {ABD} = 180^\circ - 2.30^\circ = 120^\circ \).
Áp dụng định lí côsin trong tam giác ABD ta có:
\(B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos \widehat {BAD}\)
Thay số: \(B{D^2} = {2^2} + {2^2} - 2.2.2.\cos 120^\circ = 12\)\( \Rightarrow BD = 2\sqrt 3 \)cm.