Đề thi Toán 11 Học kì 2 có đáp án (Đề 7)
-
459 lượt thi
-
34 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số y = 2\(\sqrt x - x\)với x > 0. Tính y'(1) có kết quả là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có y' = \(\frac{1}{{\sqrt x }} - 1\) Þ y'(1) = 0.
Câu 2:
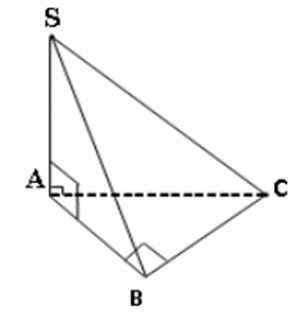
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA ^ (ABC). Chọn khẳng định đúng
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta có SA ^ (ABC) Þ SA ^ BC.
Câu 3:
Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta có: lim \({\left( {\frac{1}{4}} \right)^n}\)= 0
Câu 4:
Tổng S = 1 + \(\frac{1}{2}\)+ \(\frac{1}{4}\)+ … + \(\frac{1}{{{2^n}}}\)+ … có giá trị là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta có S = 1 + \(\frac{1}{2}\)+ \(\frac{1}{4}\)+ … + \(\frac{1}{{{2^n}}}\)+ …
Þ Sn = \(\frac{1}{2}\)+ \(\frac{1}{4}\)+ … + \(\frac{1}{{{2^n}}}\)+ Þ S = 1 + Sn
Tổng của cấp số nhân lùi vô hạn có công thức Sn = \(\frac{{{u_1}}}{{1 - q}}\)
Theo đề bài ta có u1 = \(\frac{1}{2}\), q = \(\frac{1}{2}\) Þ Sn = 1
Vậy S = 1 + 1 = 2.
Câu 5:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta có: y = 3sin2x + 2
Suy ra y' = 3.(2x)'.cos2x = 6.cos2x
Câu 6:
Mệnh đề nào sau đây sai?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Đáp án A sai vì \(\left( {\sqrt x } \right)' = \frac{1}{{2\sqrt x }}(x > 0).\)
Câu 7:
bằng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta có \(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{2x - 5}}{{x - 2}} = \frac{{2.2 - 5}}{{2 - 2}} = \frac{{ - 1}}{{{0^ - }}} = + \infty \)
Câu 8:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Đáp án A: điều kiện xác định x ≠ 1
Þ Hàm số gián đoạn tại x0 = 1.
Câu 9:
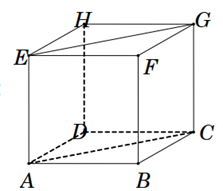
Cho hình lập phương ABCD.EFGH có cạnh bằng a. Tính \(\overrightarrow {AB} .\overrightarrow {EG} \) bằng
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có: \(\overrightarrow {AB} .\overrightarrow {EG} \)
\( = \overrightarrow {AB} .(\overrightarrow {EF} + \overrightarrow {EH} )\)
\( = \overrightarrow {AB} .\overrightarrow {EF} + \overrightarrow {AB} .\overrightarrow {EH} \)
\( = {\overrightarrow {AB} ^2} + \overrightarrow {AB} .\overrightarrow {AD} \left( {\overrightarrow {AB} = \overrightarrow {EF} ;\overrightarrow {EH} = \overrightarrow {AD} } \right)\)
\( = {\overrightarrow {AB} ^2} + \overrightarrow 0 = {a^2}\left( {\overrightarrow {AB} \bot \overrightarrow {AD} \Rightarrow \overrightarrow {AB} .\overrightarrow {AD} = \overrightarrow 0 } \right)\)
Vậy \(\overrightarrow {AB} .\overrightarrow {EG} = {a^2}\)
Câu 10:
Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{c}}{3x + 1\,\,\,\,\,\,\,\,khi\,x \ne 1}\\{2x + 2a\,\,\,\,khi\,x = 1}\end{array}} \right.\). Giá trị của a để hàm số f(x) liên tục trên ℝ là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có f(1) = 2 + 2a;
\(\mathop {\lim }\limits_{x \to 1} (3x + 1) = 3.1 + 1 = 4\).
Để f(x) liên tục trên ℝ Û f(1) = \[\mathop {\lim }\limits_{x \to 1} f(x)\]Û 2 + 2a = 4 Þ a = 1.
Câu 11:
Cho hình chóp S.ABC có SA ^ (ABC).
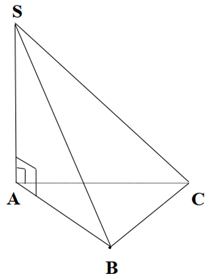
Góc giữa đường thẳng SC và mặt phẳng (ABC) là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có SA ^ (ABC) Þ AC là hình chiều của SC lên (ABC).
Þ [SC, (ABC)] = \(\widehat {SCA}\).
Câu 12:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết rằng SA = SC, SB = SD. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có:
∙ SA = SC Þ Tam giác SAC cân tại S
Þ SO là đường cao tam giác SAC Þ SO ^ AC (1)
∙ SB = SD Þ Tam giác SBD cân tại S
Þ SO là đường cao tam giác SBD Þ SO ^ BD (2)
Từ (1) và (2) suy ra SO ^ (ABCD).
Câu 13:
Giả sử u = u(x), v = v(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Đẳng thức đúng là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Đẳng thức đúng là: (uv)' = u'v + uv'
Câu 14:
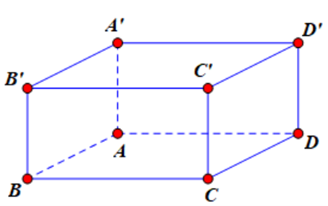
Cho hình hộp ABCD.A’B’C’D’. Khẳng định nào đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
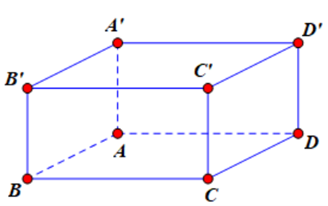
Ta có \(\overrightarrow {CB} + \overrightarrow {CD} = \overrightarrow {CA} \) (quy tắc hình bình hành); \(\overrightarrow {C'C} = \overrightarrow {AA'} \)
Þ \(\overrightarrow {CB} + \overrightarrow {CD} + \overrightarrow {C'C} = \overrightarrow {CA} + \overrightarrow {AA'} = \overrightarrow {CA'} \)
Câu 15:
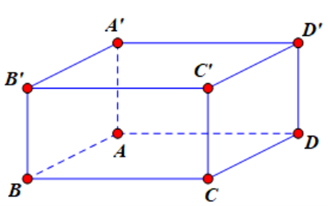
Cho hình lập phương ABCD.A’B’C’D’. Bộ ba vectơ nào sau đây đồng phẳng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
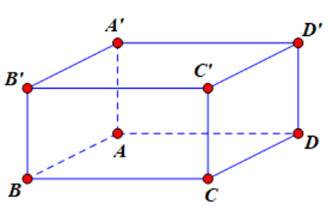
Ta thấy B’C’ // (ABCD) và A’B’ // (ABCD) nên \(\overrightarrow {B'C'} ,\overrightarrow {AD} ,\overrightarrow {A'B'} \) đồng phẳng.
Câu 16:
Trong các mệnh đề sau, mệnh đề nào sai?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta có: \(\mathop {\lim }\limits_{x \to {0^ - }} \frac{1}{{{x^2}}} = + \infty \). Vậy đáp án A sai.
Câu 17:
Giới hạn \(\mathop {\lim }\limits_{x \to - 3} \frac{{{x^2} + 4x + 3}}{{x + 3}}\) có kết quả là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta có: \(\mathop {\lim }\limits_{x \to - 3} \frac{{{x^2} + 4x + 3}}{{x + 3}}\)
\( = \mathop {\lim }\limits_{x \to - 3} \frac{{(x + 3)(x + 1)}}{{x + 3}} = \mathop {\lim }\limits_{x \to - 3} (x + 1) = - 2\).
Câu 18:
Cho hai hàm số f(x), g(x) thỏa mãn \(\mathop {\lim }\limits_{x \to 1} f(x)\)= −6 và \(\mathop {\lim }\limits_{x \to 1} g(x)\)= 3. Giá trị của \(\mathop {\lim }\limits_{x \to 1} \left[ {f(x) - g(x)} \right]\) bằng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có: \(\mathop {\lim }\limits_{x \to 1} \left[ {f(x) - g(x)} \right] = \mathop {\lim }\limits_{x \to 1} f(x) - \mathop {\lim }\limits_{x \to 1} g(x) = - 6 - 3 = - 9\).
Câu 19:
Hàm số nào sau đây liên tục trên ℝ?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Đáp án A: điều kiện xác định x2 + x – 2 ≠ 0 Û \(\left\{ {\begin{array}{*{20}{c}}{x \ne 1}\\{x \ne - 2}\end{array}} \right.\)
Þ Hàm số không liên tục trên ℝ.
Đáp án B: điều kiện xác định x + 1 ≠ 0 Û x ≠ −1
Þ Hàm số không liên tục trên ℝ.
Đáp án C: cotx = \(\frac{{\cos x}}{{\sin x}}\), điều kiện xác định sinx ≠ 0
Þ Hàm số không liên tục trên ℝ.
Đáp án D: tập xác định D = ℝ Þ Hàm số liên tục trên ℝ.
Câu 20:
Giới hạn \(\mathop {\lim }\limits_{x \to - 2} ({x^2} + x + 1)\) có kết quả là giá trị nào sau đây?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta có: \(\mathop {\lim }\limits_{x \to - 2} ({x^2} + x + 1) = {( - 2)^2} - 2 + 1 = 3\).
Câu 21:
Cho hình lập phương ABCD.EFGH có cạnh bằng a. Tính d(AB, (EFGH)).
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
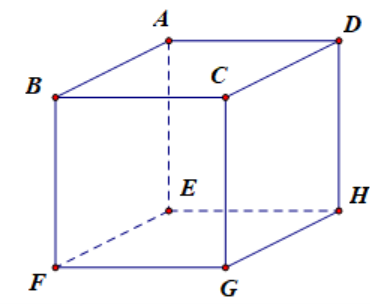
Ta có AE ^ (EFGH)
Þ d(AB,(EFGH)) = d(A,(EFGH)) = AE = a.
Câu 22:
Hàm số y = sinx có đạo hàm cấp hai là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta có: y = sinx Þ y' = −cosx Þ y" = −sinx.
Câu 23:
Trong bốn giới hạn sau đây, giới hạn nào là −1?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Đáp án A, ta có lim un = lim \(\frac{{{n^2} + n}}{{ - 2n - {n^2}}}\)= \(\lim \frac{{{n^2}\left( {1 + \frac{1}{n}} \right)}}{{{n^2}\left( {\frac{{ - 2}}{n} - 1} \right)}} = - 1.\)
Đáp án B, ta có lim un = lim\(\frac{{{n^3}}}{{{n^2} + 3}}\)= \(\lim \frac{{{n^3}}}{{{n^3}\left( {\frac{1}{n} + \frac{3}{{{n^3}}}} \right)}} = + \infty \).
Đáp án C, ta có lim un = lim\(\frac{{2n + 3}}{{2 - 3n}}\)= \(\lim \frac{{n\left( {2 + \frac{3}{n}} \right)}}{{n\left( {\frac{2}{n} - 3} \right)}} = - \frac{2}{3}\).
Đáp án D, ta có lim un = lim\(\frac{{{n^2} - {n^3}}}{{2{n^3} + 1}}\)= \(\lim \frac{{{n^3}\left( {\frac{1}{n} - 1} \right)}}{{{n^3}\left( {2 + \frac{1}{{{n^3}}}} \right)}} = - \frac{1}{2}\).
Vậy đáp án A thỏa yêu cầu bài toán.
Câu 24:
Tính đạo hàm của hàm số y = \(\frac{{x + 1}}{{x - 2}}.\) Kết quả là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có y = \(\frac{{x + 1}}{{x - 2}}\) Þ y' = \(\frac{{ - 3}}{{{{(x - 2)}^2}}}\).
Câu 25:
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \)và \(\overrightarrow {DH} \)?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
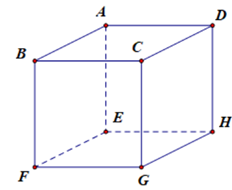
Ta có: \(\left( {\overrightarrow {AB} ,\overrightarrow {DH} } \right) = \left( {\overrightarrow {DC} ,\overrightarrow {DH} } \right) = 90^\circ \).
Câu 26:
Tính các giới hạn sau.
A = lim\(\frac{{2{n^2} - n + 2}}{{3{n^2} + 5n}}\)
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có A = lim\(\frac{{2{n^2} - n + 2}}{{3{n^2} + 5n}}\)
= lim\[\frac{{{n^2}\left( {2 - \frac{1}{n} + \frac{2}{{{n^2}}}} \right)}}{{{n^2}\left( {3 + \frac{5}{n}} \right)}}\]
\[ = \lim \frac{{2 - \frac{1}{n} + \frac{2}{{{n^2}}}}}{{3 + \frac{5}{n}}} = \frac{2}{3}.\]
Câu 27:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có B = \(\mathop {\lim }\limits_{x \to 3} \frac{{2 - \sqrt {x + 1} }}{{x - 3}} = \mathop {\lim }\limits_{x \to 3} \frac{{4 - (x + 1)}}{{(x - 3)\left( {2 + \sqrt {x + 1} } \right)}}\)
\[ = \mathop {\lim }\limits_{x \to 3} \frac{{3 - x}}{{(x - 3)\left( {2 + \sqrt {x + 1} } \right)}} = \mathop {\lim }\limits_{x \to 3} \frac{{ - 1}}{{2 + \sqrt {x + 1} }} = \frac{{ - 1}}{{2 + \sqrt {3 + 1} }} = \frac{{ - 1}}{4}.\]
Câu 28:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có \(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {a{x^2} + bx} - cx} \right) = - 2\)
\( \Leftrightarrow \mathop {\lim }\limits_{x \to + \infty } \frac{{a{x^2} + bx - {c^2}{x^2}}}{{\sqrt {a{x^2} + bx} + cx}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\left( {a - {c^2}} \right){x^2} + bx}}{{\sqrt {a{x^2} + bx} + cx}} = - 2\)
Điều này xảy ra nên \(\left\{ {\begin{array}{*{20}{c}}{a - {c^2} = 0\,\,(a,\,\,c > 0)}\\{\frac{b}{{\sqrt a + c}} = - 2\,\,(*)}\end{array}} \right..\)
Mặt khác ta cũng có c2 + a = 18.
Lập hệ phương trình ta có: \(\left\{ {\begin{array}{*{20}{c}}{ - {c^2} + a = 0}\\{{c^2} + a = 18}\end{array}} \right.\)
Û c2 = a = 9 Þ c = 3.
Thay a, c vào (*) Þ b = −12.
Vậy P = a + b + 5c = 12.
Câu 29:
Tính đạo hàm của các hàm số sau:
y = x3 – 3x + 2
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có y = x3 – 3x + 2 Þ y' = 3x2 – 3.
Câu 30:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có y = sin3(3x + 2)
Þ y' = 3sin2(3x + 2).[sin(3x + 2)]'
= 3sin2(3x + 2).(3x + 2)'.cos(3x + 2)
= 9sin2(3x + 2).cos(3x + 2).
Câu 31:
Cho hàm số y = f(x) = x2 – 2x + 4 có đồ thị (C)
Viết phương trình tiếp tuyến của đồ thị (C) tại điểm M(3; 7)
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: y' = 2x – 2 Þ y'(3) = 4.
Vậy phương trình tiếp tuyến của đồ thị (C) tại điểm M(3; 7) là y = 4(x – 3) + 7 = 4x – 5.
Câu 32:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Gọi N(x0;y0) là tiếp điểm của tiếp tuyến đồ thị (C) và ta có y' = 2x – 2.
Ta có k = 2 có nghĩa là f '(x0) = 2 Û 2x0 – 2 = 2 Û x0 = 2 Þ y0 = 4.
Vậy phương trình tiếp tuyến của đồ thị (C) tại điểm N(x0; y0) là y = 2(x – 2) + 4 = 2x.
Câu 33:
Cho hình chóp S.ABC có đáy là tam giác đều cạnh 4a. Biết SB vuông góc với mặt đáy, P là trung điểm của cạnh AC.
Chứng minh rằng AC ^ (SBP).
 Xem đáp án
Xem đáp án
Hướng dẫn giải
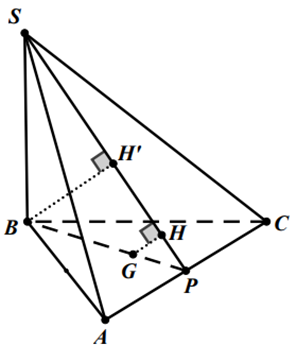
Ta có: AC ^ BP (vì ∆ABC đều);
AC ^ SB (vì SB ^ (ABC))
Do đó AC ^ (SBP).
Câu 34:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Gọi H, H’ lần lượt là hình chiếu của G và B lên SP.
Ta có BP ^ AC, SP ^ AC Þ \(\left( {(SAC),(ABC)} \right) = \widehat {SPB} = 60^\circ \)
Ta lại có \(\frac{{GH}}{{BH'}} = \frac{{GP}}{{BP}} = \frac{1}{3} \Rightarrow GH = \frac{1}{3}BH'\)
Þ d[G,(SAC)] = \(\frac{1}{3}\)d[B,(SAC)]
Ta có BP = \(\frac{{4a\sqrt 3 }}{2}\)= 2a\(\sqrt 3 \) (đường cao tam giác đều)
SB = tan\(\widehat {SPB}\).BP = tan60. 2a\(\sqrt 3 \) = 6a
BH’ = \(\frac{{SB.BP}}{{\sqrt {S{B^2} + B{P^2}} }} = \frac{{6a.2a\sqrt 3 }}{{\sqrt {{{(6a)}^2} + {{\left( {2a\sqrt 3 } \right)}^2}} }} = 3a\)
Vậy d[G,(SAC)] = \(\frac{1}{3}\).3a = a.
