Câu hỏi:
03/04/2024 35Tổng S = 1 + \(\frac{1}{2}\)+ \(\frac{1}{4}\)+ … + \(\frac{1}{{{2^n}}}\)+ … có giá trị là
A. S = \(\frac{3}{4}\)
B. S = \(\frac{3}{2}\)
C. S = 3
D. S = 2
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
Ta có S = 1 + \(\frac{1}{2}\)+ \(\frac{1}{4}\)+ … + \(\frac{1}{{{2^n}}}\)+ …
Þ Sn = \(\frac{1}{2}\)+ \(\frac{1}{4}\)+ … + \(\frac{1}{{{2^n}}}\)+ Þ S = 1 + Sn
Tổng của cấp số nhân lùi vô hạn có công thức Sn = \(\frac{{{u_1}}}{{1 - q}}\)
Theo đề bài ta có u1 = \(\frac{1}{2}\), q = \(\frac{1}{2}\) Þ Sn = 1
Vậy S = 1 + 1 = 2.
Hướng dẫn giải
Đáp án đúng là: D
Ta có S = 1 + \(\frac{1}{2}\)+ \(\frac{1}{4}\)+ … + \(\frac{1}{{{2^n}}}\)+ …
Þ Sn = \(\frac{1}{2}\)+ \(\frac{1}{4}\)+ … + \(\frac{1}{{{2^n}}}\)+ Þ S = 1 + Sn
Tổng của cấp số nhân lùi vô hạn có công thức Sn = \(\frac{{{u_1}}}{{1 - q}}\)
Theo đề bài ta có u1 = \(\frac{1}{2}\), q = \(\frac{1}{2}\) Þ Sn = 1
Vậy S = 1 + 1 = 2.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Giả sử u = u(x), v = v(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Đẳng thức đúng là
Câu 2:
Gọi G là trọng tâm của tam giác ABC. Tính khoảng cách từ điểm G đến mặt phẳng (SAC), biết góc tạo bởi (SAC) và mặt phẳng (ABC) bằng 60°.
Câu 3:
B = \(\mathop {\lim }\limits_{x \to 3} \frac{{2 - \sqrt {x + 1} }}{{x - 3}}\).
Câu 5:
Cho hình chóp S.ABC có đáy là tam giác đều cạnh 4a. Biết SB vuông góc với mặt đáy, P là trung điểm của cạnh AC.
Chứng minh rằng AC ^ (SBP).
Cho hình chóp S.ABC có đáy là tam giác đều cạnh 4a. Biết SB vuông góc với mặt đáy, P là trung điểm của cạnh AC.
Chứng minh rằng AC ^ (SBP).
Câu 6:
Tính đạo hàm của hàm số y = \(\frac{{x + 1}}{{x - 2}}.\) Kết quả là
Câu 12:
Cho hình chóp S.ABC có SA ^ (ABC).
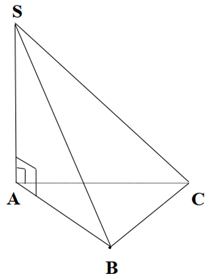
Góc giữa đường thẳng SC và mặt phẳng (ABC) là
Cho hình chóp S.ABC có SA ^ (ABC).

Góc giữa đường thẳng SC và mặt phẳng (ABC) là
Câu 14:
Cho hàm số y = f(x) = x2 – 2x + 4 có đồ thị (C)
Viết phương trình tiếp tuyến của đồ thị (C) tại điểm M(3; 7)
Cho hàm số y = f(x) = x2 – 2x + 4 có đồ thị (C)
Viết phương trình tiếp tuyến của đồ thị (C) tại điểm M(3; 7)
Câu 15:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết rằng SA = SC, SB = SD. Khẳng định nào sau đây là đúng?