Câu hỏi:
03/04/2024 40
Cho hình chóp S.ABCD, đáy ABCD là hình thang có \(A{\rm{D // BC}}{\rm{, AB}} = BC = a\), \(BA{\rm{D}} = 60^\circ \).
a) Gọi M là trung điểm SD. Lấy điểm N nằm trên cạnh SA sao cho \(SN = 2NA\). Tìm giao điểm H của đường thẳng MN và mặt phẳng \(\left( {ABC{\rm{D}}} \right)\).
b) Gọi G là trọng tâm tam giác SAB. Mặt phẳng \(\left( \alpha \right)\) đi qua G và song song với hai đường thẳng AB, CD. Tính chu vi thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng \(\left( \alpha \right)\).
Cho hình chóp S.ABCD, đáy ABCD là hình thang có \(A{\rm{D // BC}}{\rm{, AB}} = BC = a\), \(BA{\rm{D}} = 60^\circ \).
a) Gọi M là trung điểm SD. Lấy điểm N nằm trên cạnh SA sao cho \(SN = 2NA\). Tìm giao điểm H của đường thẳng MN và mặt phẳng \(\left( {ABC{\rm{D}}} \right)\).
b) Gọi G là trọng tâm tam giác SAB. Mặt phẳng \(\left( \alpha \right)\) đi qua G và song song với hai đường thẳng AB, CD. Tính chu vi thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng \(\left( \alpha \right)\).
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
a) \(\left\{ \begin{array}{l}a \cap b = M\\b \subset \left( P \right)\end{array} \right. \Rightarrow a \cap \left( P \right) = M\).
b) Xác định mặt phẳng \(\left( \alpha \right)\).
Sử dụng định lí Cosin trong tam giác và định lí Ta-lét tính độ dài các cạnh của thiết diện, từ đó tính chu vi thiết diện.
Cách giải:
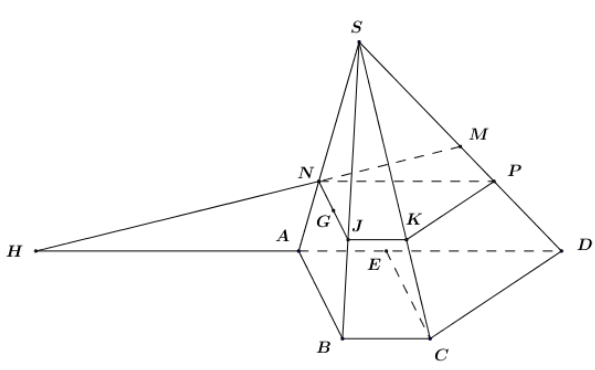
a) Trong mặt phẳng \(\left( {SA{\rm{D}}} \right)\) gọi: \(MN \cap A{\rm{D}} = H\).
Ta có \(\left\{ \begin{array}{l}H \in MN\\H \in {\rm{AD}} \subset \left( {ABC{\rm{D}}} \right) \Rightarrow H \in \left( {ABC{\rm{D}}} \right)\end{array} \right. \Rightarrow H = MN \cap \left( {ABC{\rm{D}}} \right)\).
b) Trong \(\left( {SAB} \right)\) qua G kẻ đường thẳng \(NJ{\rm{ // AB }}\left( {N \in SA,J \in SB} \right)\), ta có:
\(\left\{ \begin{array}{l}G \in \left( \alpha \right) \cap \left( {SAB} \right)\\\left( \alpha \right){\rm{ // AB}} \subset \left( {SAB} \right)\end{array} \right. \Rightarrow \left( \alpha \right) \cap \left( {SAB} \right) = NJ\).
Trong \(\left( {SBC} \right)\) qua J kẻ \(JK{\rm{ // BC }}\left( {K \in SC} \right)\), CMTT ta có \(\left( \alpha \right) \cap \left( {SBC} \right) = JK\).
Trong \(\left( {SA{\rm{D}}} \right)\) qua N kẻ \(NP{\rm{ // AD }}\left( {P \in SD} \right)\), ta có \(\left( \alpha \right) \cap \left( {SA{\rm{D}}} \right) = NP\) và \(\left( \alpha \right) \cap \left( {SBC} \right) = PK\).
Do đó thiết diện của chóp cắt bởi \(\left( \alpha \right)\) là tứ giác NJKP.
Qua C kẻ đường thẳng song song với BA cắt AD tại E.
Dễ dàng chứng minh được ABCE là hình bình hành \( \Rightarrow A{\rm{E}} = BC = a \Rightarrow E{\rm{D}} = AB - A{\rm{E}} = 2{\rm{a}}\).
Lại có \(BA{\rm{D}} = 60^\circ \Rightarrow CE{\rm{D}} = 60^\circ \) (đồng vị).
Xét tam giác CED áp dụng định lý Cosin ta có:
\(C{{\rm{D}}^2} = C{E^2} + D{E^2} - 2CE.DE\cos \left( {CED} \right)\)
\( \Rightarrow C{D^2} = {a^2} + {\left( {2a} \right)^2} - 2 \times a \times 2a \times \cos \left( {60^\circ } \right)\)
\( \Rightarrow C{D^2} = 3{a^2} \Rightarrow CD = a\sqrt 3 \).
Mặt khác: \(\left\{ \begin{array}{l}SN = 2NA \Rightarrow \frac{{SN}}{{SA}} = \frac{2}{3}\\AB{\rm{ // NJ}}{\rm{, BC // JK}}{\rm{, CD // KP}}{\rm{, DA // PN}}\end{array} \right.\)
\( \Rightarrow NJ = \frac{2}{3}AB = \frac{2}{3}a\)
\(JK = \frac{2}{3}BC = \frac{2}{3}a\)
\(NP = \frac{2}{3}A{\rm{D}} = 2{\rm{a}}\)
\(KP = \frac{2}{3}C{\rm{D}} = \frac{{2\sqrt 3 }}{3}a\).
Chu vi thiết diện NJKP bằng: \(NJ + JK + NP + KP = \frac{2}{3}a + \frac{2}{3}a + 2{\rm{a}} + \frac{{2\sqrt 3 }}{3}a = \frac{{10 + 2\sqrt 3 }}{3}a\).
Phương pháp:
a) \(\left\{ \begin{array}{l}a \cap b = M\\b \subset \left( P \right)\end{array} \right. \Rightarrow a \cap \left( P \right) = M\).
b) Xác định mặt phẳng \(\left( \alpha \right)\).
Sử dụng định lí Cosin trong tam giác và định lí Ta-lét tính độ dài các cạnh của thiết diện, từ đó tính chu vi thiết diện.
Cách giải:

a) Trong mặt phẳng \(\left( {SA{\rm{D}}} \right)\) gọi: \(MN \cap A{\rm{D}} = H\).
Ta có \(\left\{ \begin{array}{l}H \in MN\\H \in {\rm{AD}} \subset \left( {ABC{\rm{D}}} \right) \Rightarrow H \in \left( {ABC{\rm{D}}} \right)\end{array} \right. \Rightarrow H = MN \cap \left( {ABC{\rm{D}}} \right)\).
b) Trong \(\left( {SAB} \right)\) qua G kẻ đường thẳng \(NJ{\rm{ // AB }}\left( {N \in SA,J \in SB} \right)\), ta có:
\(\left\{ \begin{array}{l}G \in \left( \alpha \right) \cap \left( {SAB} \right)\\\left( \alpha \right){\rm{ // AB}} \subset \left( {SAB} \right)\end{array} \right. \Rightarrow \left( \alpha \right) \cap \left( {SAB} \right) = NJ\).
Trong \(\left( {SBC} \right)\) qua J kẻ \(JK{\rm{ // BC }}\left( {K \in SC} \right)\), CMTT ta có \(\left( \alpha \right) \cap \left( {SBC} \right) = JK\).
Trong \(\left( {SA{\rm{D}}} \right)\) qua N kẻ \(NP{\rm{ // AD }}\left( {P \in SD} \right)\), ta có \(\left( \alpha \right) \cap \left( {SA{\rm{D}}} \right) = NP\) và \(\left( \alpha \right) \cap \left( {SBC} \right) = PK\).
Do đó thiết diện của chóp cắt bởi \(\left( \alpha \right)\) là tứ giác NJKP.
Qua C kẻ đường thẳng song song với BA cắt AD tại E.
Dễ dàng chứng minh được ABCE là hình bình hành \( \Rightarrow A{\rm{E}} = BC = a \Rightarrow E{\rm{D}} = AB - A{\rm{E}} = 2{\rm{a}}\).
Lại có \(BA{\rm{D}} = 60^\circ \Rightarrow CE{\rm{D}} = 60^\circ \) (đồng vị).
Xét tam giác CED áp dụng định lý Cosin ta có:
\(C{{\rm{D}}^2} = C{E^2} + D{E^2} - 2CE.DE\cos \left( {CED} \right)\)
\( \Rightarrow C{D^2} = {a^2} + {\left( {2a} \right)^2} - 2 \times a \times 2a \times \cos \left( {60^\circ } \right)\)
\( \Rightarrow C{D^2} = 3{a^2} \Rightarrow CD = a\sqrt 3 \).
Mặt khác: \(\left\{ \begin{array}{l}SN = 2NA \Rightarrow \frac{{SN}}{{SA}} = \frac{2}{3}\\AB{\rm{ // NJ}}{\rm{, BC // JK}}{\rm{, CD // KP}}{\rm{, DA // PN}}\end{array} \right.\)
\( \Rightarrow NJ = \frac{2}{3}AB = \frac{2}{3}a\)
\(JK = \frac{2}{3}BC = \frac{2}{3}a\)
\(NP = \frac{2}{3}A{\rm{D}} = 2{\rm{a}}\)
\(KP = \frac{2}{3}C{\rm{D}} = \frac{{2\sqrt 3 }}{3}a\).
Chu vi thiết diện NJKP bằng: \(NJ + JK + NP + KP = \frac{2}{3}a + \frac{2}{3}a + 2{\rm{a}} + \frac{{2\sqrt 3 }}{3}a = \frac{{10 + 2\sqrt 3 }}{3}a\).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong mặt phẳng Oxy, cho đường tròn \(\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} = 9\). Ảnh của đường tròn \(\left( C \right)\) qua phép vị tự tâm \(I\left( {3;2} \right)\), tỉ số 2 là đường tròn có phương trình?
Câu 2:
Ông Nam đã trồng cây ca cao trên mảnh đất của mình có dạng hình tam giác, ông trồng ở hàng đầu tiên 3 cây ca cao, kể từ hàng thứ hai trở đi số cây phải trồng ở mỗi hàng nhiều hơn 5 cây so với số cây đã trồng ở hàng trước đó và ở hàng cuối cùng ông đã trồng 2018 cây ca cao. Số cây ca cao mà ông Nam đã trồng trên mảnh đất của mình là
Câu 3:
Từ các chữ số của tập \(X = \left\{ {1;2;4;5;7;8} \right\}\) có thể lập được bao nhiêu số tự nhiên có bốn chữ số đôi một khác nhau?
Câu 4:
Cho lục giác đều ABCDEF tâm O như hình vẽ. Thực hiện liên tiếp phép quay tâm O, góc quay \(120^\circ \) và phép quay vị tự tâm O, tỉ số \( - 1\) đối với một tam giác trong lục giác đều trên ta được ảnh là tam giác OBC. Tạo ảnh của tam giác OBC là?
Câu 5:
Trong đề cương ôn tập bộ môn Toán có 15 câu hỏi Đại số và 10 câu hỏi Hình học. Hỏi có bao nhiêu cách chọn ngẫu nhiên 5 câu hỏi có cả Đại số và Hình học để lập một đề kiểm tra 15 phút?
Câu 6:
Trong hộp có 13 quả bóng bàn được đánh số từ 1 đến 13. Lấy ngẫu nhiên 6 quả bóng bàn trong hộp. Xác xuất để tổng số ghi trên 6 quả bóng bàn được lấy ra chia hết cho 2 là?
Câu 7:
Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi. Gọi O là giao điểm của AC và BD, M là giao điểm của AB và CD, N là giao điểm của AD và BC. Giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SC{\rm{D}}} \right)\) là?
Câu 8:
Nghiệm của phương trình \({\tan ^2}3{\rm{x}} - \left( {\sqrt 3 - 1} \right)\tan 3{\rm{x}} - \sqrt 3 = 0\) là?
Câu 9:
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. G là trung điểm của MN, I là giao điểm của đường thẳng AG và mặt phẳng \(\left( {BC{\rm{D}}} \right)\). Tính tỉ số \(\frac{{GI}}{{GA}}\)?
Câu 11:
Giá trị của tham số m để phương trình \(\left( {\sin x + \cos x - 1} \right)\left( {\sin 4x - m} \right) = 0\) có đúng bốn nghiệm phân biệt thuộc đoạn \(\left[ {\frac{\pi }{8};\frac{{5\pi }}{6}} \right]\) là \(m \in \left[ {a;b} \right)\backslash \left\{ c \right\}\). Khi đó, giá trị biểu thức \({a^2} + 2b + c\) bằng?
Câu 12:
Trong mặt phẳng Oxy, cho đường thẳng \(\Delta :2{\rm{x}} - 3y - 5 = 0\). Ảnh của đường Δ qua phép tịnh tiến theo vectơ \(\overrightarrow u = \left( { - 1;2} \right)\) là đường thẳng nào?
Câu 13:
a) (0,5 điểm) Đoàn học sinh tham gia Hội thao Giáo dục quốc phòng và an ninh học sinh THPT cấp tỉnh lần thứ V năm 2018 của một trường THPT gồm có 8 học sinh nam và 7 học sinh nữ. Chọn ngẫu nhiên 9 học sinh để tham gia bộ môn thi điều lệnh. Tính xác suất để trong 9 học sinh được chọn ra có đúng 5 học sinh nam.
a) (0,5 điểm) Đoàn học sinh tham gia Hội thao Giáo dục quốc phòng và an ninh học sinh THPT cấp tỉnh lần thứ V năm 2018 của một trường THPT gồm có 8 học sinh nam và 7 học sinh nữ. Chọn ngẫu nhiên 9 học sinh để tham gia bộ môn thi điều lệnh. Tính xác suất để trong 9 học sinh được chọn ra có đúng 5 học sinh nam.


